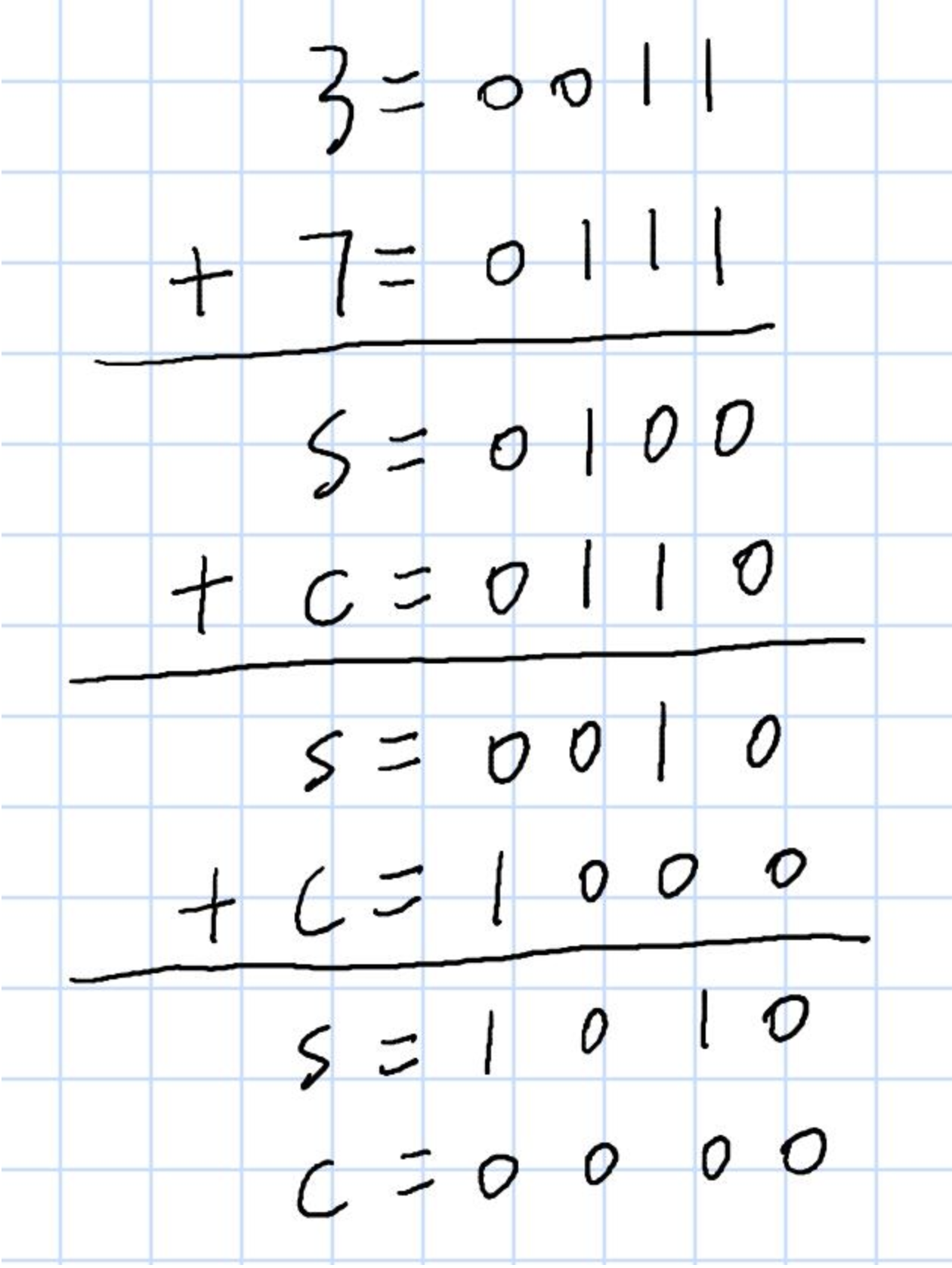索引
剑指Offer
Hash 1_twoSum 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import timeitclass Solution : def twoSum (self, nums, target ): hashmap = {} for loc, num in enumerate (nums): if hashmap.get(target - num) is not None : return [hashmap.get(target - num), loc] hashmap[num] = loc return None nums = [2 , 7 , 3 , 6 , 5 ] so = Solution() start = timeit.default_timer() print(so.twoSum(nums, 8 )) end = timeit.default_timer() print(str ((end - start) * 1000 ), "s" )
valid-sudoku 解题思路:
行中没有重复的数字。
列中没有重复的数字。
3 x 3 子数独内没有重复的数字。
可以使用 box_index = (row // 3) * 3 + columns // 3作为子数独的索引号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class Solution : def isValidSudoku (self, board ) -> bool: rows = [{} for i in range (0 , 9 )] columns = [{} for i in range (0 , 9 )] boxes = [{} for i in range (0 , 9 )] for row in range (0 , 9 ): for column in range (0 , 9 ): number = board[row][column] if number != "." : number = int (number) box_index = (row // 3 ) * 3 + column // 3 rows[row][number] = rows[row].get(number, 0 ) + 1 columns[column][number] = columns[column].get(number, 0 ) + 1 boxes[box_index][number] = boxes[box_index].get(number, 0 ) + 1 if rows[row][number] > 1 or columns[column][number] > 1 or boxes[box_index][number] > 1 : return False return True so = Solution() print(so.isValidSudoku([ ["8" , "3" , "." , "." , "7" , "." , "." , "." , "." ], ["6" , "." , "." , "1" , "9" , "5" , "." , "." , "." ], ["." , "9" , "8" , "." , "." , "." , "." , "6" , "." ], ["8" , "." , "." , "." , "6" , "." , "." , "." , "3" ], ["4" , "." , "." , "8" , "." , "3" , "." , "." , "1" ], ["7" , "." , "." , "." , "2" , "." , "." , "." , "6" ], ["." , "6" , "." , "." , "." , "." , "2" , "8" , "." ], ["." , "." , "." , "4" , "1" , "9" , "." , "." , "5" ], ["." , "." , "." , "." , "8" , "." , "." , "7" , "9" ] ])) print(so.isValidSudoku([ ["5" , "3" , "." , "." , "7" , "." , "." , "." , "." ], ["6" , "." , "." , "1" , "9" , "5" , "." , "." , "." ], ["." , "9" , "8" , "." , "." , "." , "." , "6" , "." ], ["8" , "." , "." , "." , "6" , "." , "." , "." , "3" ], ["4" , "." , "." , "8" , "." , "3" , "." , "." , "1" ], ["7" , "." , "." , "." , "2" , "." , "." , "." , "6" ], ["." , "6" , "." , "." , "." , "." , "2" , "8" , "." ], ["." , "." , "." , "4" , "1" , "9" , "." , "." , "5" ], ["." , "." , "." , "." , "8" , "." , "." , "7" , "9" ] ] ))
first-missing-positive 解题思路:使用索引作为哈希键 以及 元素的符号作为哈希值 来实现是否存在的检测。
例如,nums[2] 元素的负号意味着数字 2 出现在 nums 中。nums[3]元素的正号表示 3 没有出现在 nums 中。
解题步骤:
检查 1 是否存在于数组中。如果没有,则已经完成,1 即为答案。
如果 nums = [1],答案即为 2 。
第一次遍历:将负数,零,和大于 n 的数替换为 1 。
第二次遍历:遍历数组。当读到数字 a 时,替换第 a 个元素的符号。注意重复元素:只能改变一次符号。由于没有下标 n ,使用下标 0 的元素保存是否存在数字 n。
第三次遍历:返回第一个正数元素的下标。
如果 nums[0] > 0,则返回 n 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 from typing import Listclass Solution : def firstMissingPositive (self, nums: List[int ] ) -> int: len_nums = len (nums) if 1 not in nums: return 1 if len_nums == 1 : return 2 for i in range (0 , len_nums): if nums[i] <= 0 or nums[i] >= len_nums: nums[i] = 1 for i in range (0 , len_nums): val = abs (nums[i]) nums[val] = -abs (nums[val]) for i in range (1 , len_nums): if nums[i] > 0 : return i if nums[0 ] > 0 : return len_nums else : return len_nums + 1 so = Solution() print(so.firstMissingPositive([7 , 8 , 9 , 11 , 12 ]))
interview_28
Hash法:时间复杂度O(n)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 from typing import Listclass Solution : def majorityElement (self, nums: List[int ] ) -> int: if not nums: return 0 count_dict = dict () len_nums = len (nums) for i in range (len_nums): count_dict[nums[i]] = count_dict.setdefault(nums[i], 0 ) + 1 result_count = 0 for key in count_dict.keys(): if count_dict[key] > result_count: result_count, result_key = count_dict[key], key if result_count >= (len_nums // 2 ): return result_key return 0 so = Solution() print(so.majorityElement([1 , 2 , 3 , 2 , 2 , 2 , 5 , 4 , 2 ]))
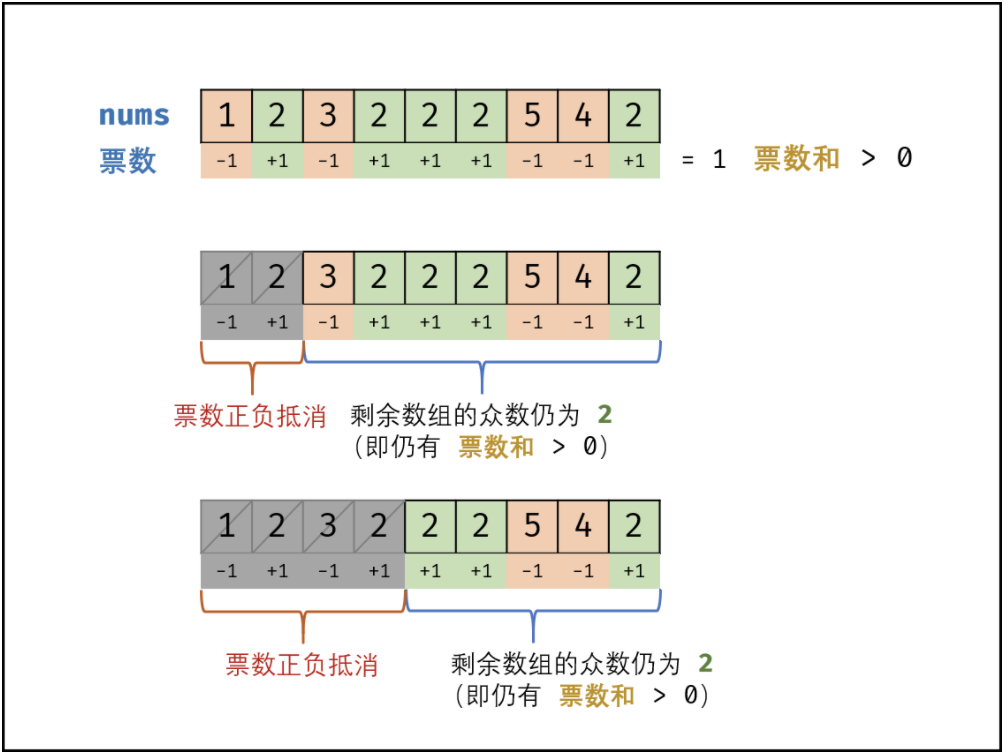
摩尔投票法
解题思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def majorityElement (self, nums: List[int ] ) -> int: if not nums: return 0 votes = 0 count = 0 for num in nums: if votes == 0 : x = num votes += 1 if num == x else -1 for _ in nums: if _ == x: count += 1 return x if count > len (nums) // 2 else 0 so = Solution() print(so.majorityElement([1 , 2 , 3 , 2 , 2 , 2 , 5 , 4 , 2 ]))
interview_34
遍历字符串 s ,使用哈希表统计 “各字符数量是否 >1 ”。
再遍历字符串 s ,在哈希表中找到首个 “数量为 1 的字符”,并返回。
Python 3.6 后,默认字典就是有序的,因此无需使用 OrderedDict()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def firstUniqChar (self, s: str ) -> str: result_dict = {} for item in s: result_dict[item] = item not in result_dict for k, v in result_dict.items(): if v: return k return " " so = Solution() print(so.firstUniqChar("NXWtnzyoHoBhUJaPauJaAitLWNMlkKwDYbbigdMMaYfkVPhGZcrEwp" ))
LinkNode 2_add_two_numbers 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def addTwoNumbers (self, l1: ListNode, l2: ListNode ) -> ListNode: if l1 is None and l2 is None : return None elif l1 is None : return l2 elif l2 is None : return l1 flag = 0 tmp = ListNode(0 ) res = tmp while l1 or l2: tmp_sum = 0 if l1: tmp_sum += l1.val l1 = l1.next if l2: tmp_sum += l2.val l2 = l2.next flag = (tmp_sum + flag) // 10 tmp_sum = (tmp_sum + flag) % 10 res.next = ListNode(tmp_sum) res = res.next if flag: res.mext = ListNode(1 ) res = tmp.next del tmp return res
merge-two-sorted-lists 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def mergeTwoLists (self, l1: ListNode, l2: ListNode ) -> ListNode: head_pre = ListNode(-1 ) pre = head_pre while l1 or l2: if l1.value < l2.value: pre.next = l1 l1 = l1.next else : pre.next = l2 l2 = l2.next pre = pre.next pre.next = l1 if l1 is not None else l2 return head_pre.next
swap-nodes-in-pairs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def swapPairs (self, head: ListNode ) -> ListNode: head_pre = ListNode(-1 ) head_pre.next = head tmp = head_pre while tmp.next and tmp.next .next : a, b = tmp.next , tmp.next .next tmp.next , a.next = b, b.next b.next = a tmp = tmp.next .next return head_pre.next
reverse-nodes-in-k-group 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def reverseKGroup (self, head: ListNode, k: int ) -> ListNode: tmp_head = ListNode(0 ) tmp_head.next = head pre = tail = tmp_head while True : count = k while count and tail: count -= 1 tail = tail.next if not tail: break head = pre.next while pre.next != tail: current_node = pre.next pre.next = current_node.next current_node.next = tail.next tail.next = current_node pre = pre.next pre, tail = head return tmp_head.next
rotate-list 解题思路:
先需旋转链表,假设旋转的步长k=2,首先循环链表得到链表的长度length_of_nodes
graph LR
id2((1)) --> id3((2))
id3((2)) --> id4((3))
id4((3)) --> id5((4))
id5((4)) --> id6((5))
id6((5)) --> id7((6))
得到倒数第二个节点的索引为length_of_nodes - k,即为新的头节点
新的尾节点的索引为length_of_nodes - k - 1
如果k>n:
那么新的头节点的索引为length_of_nodes - k % length_of_nodes
新的尾节点的索引为length_of_nodes - k % length_of_nodes - 1
graph LR
id2((1)) --> id3((2))
id3((2)) --> id4((3))
id4((3)) --> id5((4))
id5((4)) -.end.-> id6((5))
id6((5)) --> id7((6))
id7((6)) --> id2((1))
串联成新的链表
graph LR
id2((1)) --> id3((2))
id3((2)) --> id4((3))
id4((3)) --> id5((4))
id6((5)) --> id7((6))
id7((6)) --> id2((1))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def rotateRight (self, head: ListNode, k: int ) -> ListNode: if not head or head.next : return head length_of_nodes = 1 old_tail = head while old_tail.next : length_of_nodes += 1 old_tail = old_tail.next old_tail.next = head new_tail = head for i in range (length_of_nodes - k % length_of_nodes - 1 ): new_tail = new_tail.next new_head = new_tail.next return new_head
remove-duplicates-from-sorted-list-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def deleteDuplicates (self, head: ListNode ) -> ListNode: tmp_head = ListNode("head" ) tmp_head.next = head pre, cur = None , tmp_head while cur: pre = cur cur = cur.next while cur and cur.next and cur.next .val == cur.val: value = cur.val while cur and cur.val == value: cur = cur.next pre.next = cur return tmp_head.next first_node = ListNode(0 ) first_node.next = ListNode(2 ) first_node.next .next = ListNode(2 ) print(first_node.val, first_node.next .val, first_node.next .next .val) so = Solution() last_node = so.deleteDuplicates(first_node) while last_node: print(last_node.val) last_node = last_node.next
remove-duplicates-from-sorted-list 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def deleteDuplicates (self, head: ListNode ) -> ListNode: tmp = head while tmp and tmp.next : if tmp.val == tmp.next .val: tmp.next = tmp.next .next else : tmp = tmp.next return head first_node = ListNode(0 ) first_node.next = ListNode(2 ) first_node.next .next = ListNode(2 ) print(first_node.val, first_node.next .val, first_node.next .next .val) so = Solution() last_node = so.deleteDuplicates(first_node) while last_node: print(last_node.val) last_node = last_node.next
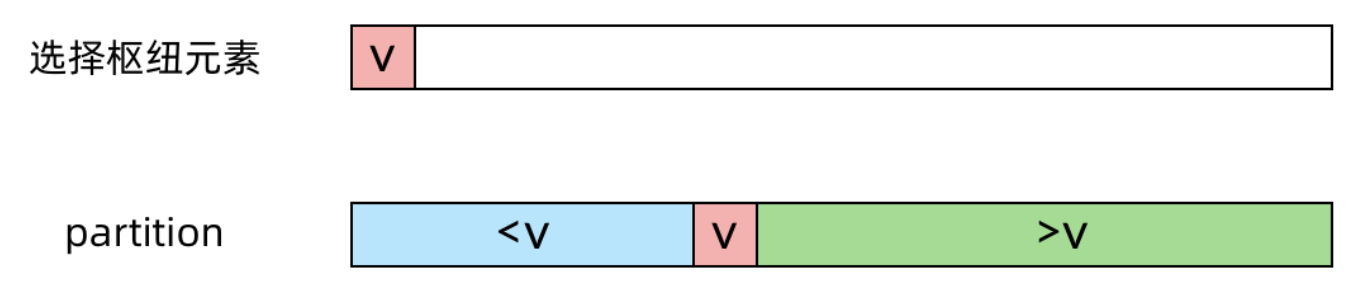
partition-list 解题思路:
before,after分别指向链表中值小于x的节点
创建before,after的哑节点:before_node、after_node
遍历链表,最后进行合并
after.next = None
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def partition (self, head: ListNode, x: int ) -> ListNode: if not head: return head before = before_node = ListNode(0 ) after = after_node = ListNode(0 ) while head: if head.val > x: after.next = head after = after.next else : before.next = head before = before.next head = head.next after.next = None before.next = after_node.next return before_node.next
reverse-linked-list-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def reverseBetween (self, head, m, n ): """ :type head: ListNode :type m: int :type n: int :rtype: ListNode """ if m == n: return head dummy = ListNode(-1 ) dummy.next = head a, d = dummy, dummy for _ in range (m - 1 ): a = a.next for _ in range (n): d = d.next b, c = a.next , d.next pre = b cur = pre.next while cur != c: cur.next , pre, cur = pre, cur, cur.next a.next = d b.next = c return dummy.next head = ListNode(1 ) head.next = ListNode(2 ) head.next .next = ListNode(3 ) head.next .next .next = ListNode(4 ) head_tmp = head while head_tmp: print(head_tmp.val) head_tmp = head_tmp.next so = Solution() return_head = so.reverseBetween(head, 2 , 3 ) return_head_tmp = return_head while return_head_tmp: print(return_head_tmp.val) return_head_tmp = return_head_tmp.next
从头到尾打印链表
解题思路:从头到尾打印,考虑使用栈结构,也可以进行递归,但是当数据量比较大时,可能出现栈溢出 ,所以直接使用栈更合适。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def printListFromTailToHead (self, list_node: ListNode ): stack = [] while list_node: stack.append(list_node.val) list_node = list_node.next while stack: print(stack.pop())
interview_25 解题思路
1 2 3 4 5 6 7 8 9 10 11 12 “”“第一部分”“” def dfs (head ): if not head: return None if head in visited: return visited[head] copy = Node(head.val, None , None ) visited[head] = copy copy.next = dfs(head.next ) “”“第二部分”“” copy.random = dfs(head.random) return copy
首先反复运行第一部分,copy.next = dfs(head.next) 会递归得越来越深,,当 碰到 head == None 时,开始运行第二部分,准备从尾结点回溯;
回溯时,先从尾结点开始回溯:调用dfs(head.ranom)时,由于结点都保存在了哈希表中,因此 return visited[head],这时完成random指针,完成了最后一个结点,故return copy。再进行倒数第二个结点的回溯:调用dfs(head.random),return visited[head],return copy…….
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Node : def __init__ (self, x: int , next : 'Node' = None , random: 'Node' = None ): self.val = int (x) self.next = next self.random = random class Solution : def copyRandomList (self, head: 'Node' ) -> 'Node': def dfs (head ): if not head: return None if head in visited: return visited[head] copy = Node(head.val, None , None ) visited[head] = copy copy.next = dfs(head.next ) copy.random = dfs(head.random) return copy visited = {} return dfs(head)
interview_3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def printListFromTailToHead (self, list_node: ListNode ): stack = [] while list_node: stack.append(list_node.val) list_node = list_node.next while stack: print(stack.pop())
interview_14 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution : def FindKthToTail (self, head, k ): if not head: return None p = head q = head count = 0 while p: p = p.next count += 1 if count >= k + 1 : q = q.next if k > count: return None return q
interview_15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def reverseList (self, head: ListNode ) -> ListNode: if not head or not head.next : return None pre_node = None current_node = head while current_node: current_node.next , pre_node, current_node = ( pre_node, current_node, current_node.next , ) return pre_node first_node = ListNode(0 ) first_node.next = ListNode(1 ) first_node.next .next = ListNode(2 ) print(first_node.val, first_node.next .val, first_node.next .next .val) so = Solution() last_node = so.reverseList(first_node) print(last_node.val, last_node.next .val, last_node.next .next .val)
interview_16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def mergeTwoLists (self, l1: ListNode, l2: ListNode ) -> ListNode: head_pre = ListNode(-1 ) pre = head_pre while l1 and l2: if l1.val < l2.val: pre.next = l1 l1 = l1.next else : pre.next = l2 l2 = l2.next pre = pre.next pre.next = l1 if l1 is not None else l2 return head_pre.next
interview_25 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Node : def __init__ (self, x: int , next : "Node" = None , random: "Node" = None ): self.val = int (x) self.next = next self.random = random class Solution : def copyRandomList (self, head: "Node" ) -> "Node": def dfs (head ): if not head: return None if head in visited: return visited[head] copy = Node(head.val, None , None ) visited[head] = copy copy.next = dfs(head.next ) copy.random = dfs(head.random) return copy visited = {} return dfs(head)
interview_36 直观思路:先统计出两个链表的长度;然后让长度较长的那个链表先走Len个节点,Len表示长度差。from this
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def getIntersectionNode (self, headA: ListNode, headB: ListNode ) -> ListNode: temphead = headA lenA = 0 while temphead: temphead = temphead.next lenA += 1 temphead = headB lenB = 0 while temphead: temphead = temphead.next lenB += 1 dLen = abs (lenA-lenB) if lenA - lenB >= 0 : headl,heads = headA,headB else : headl,heads = headB,headA while dLen > 0 : headl = headl.next dLen -= 1 while headl and heads: if headl == heads: return headl headl = headl.next heads = heads.next return None
进阶思路:两个链表长度分别为L1+C、L2+C, C为公共部分的长度。node1走了L1+C步后,回到node2起点走L2步;node2走了L2+C步后,回到node1起点走L1步。 当两个node走的步数都为L1+L2+C时就两个node就相遇了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def getIntersectionNode (self, headA: ListNode, headB: ListNode ) -> ListNode: if not headA or not headB: return None node1, node2 = headA, headB while node1 != node2: node1 = node1.next if node1 else headB node2 = node2.next if node2 else headA return node1
interview_55 两个结论:(参考链接 )
设置快慢指针,假如有环,他们最后一定相遇在环中。
两个指针相遇后,让两个指针分别从链表头和相遇点重新出发,每次走一步,最后一定相遇于环入口。
证明结论1 :设置快慢指针fast和slow,fast每次走两步,low每次走一步。假如有环,两者一定在环中相遇。(因为low指针一旦进环,可以看作是fast指针在追slow指针,因为fast指针每次走两步,slow指针每次走一步,所以最后一定能追上(相遇))。
证明结论2 :
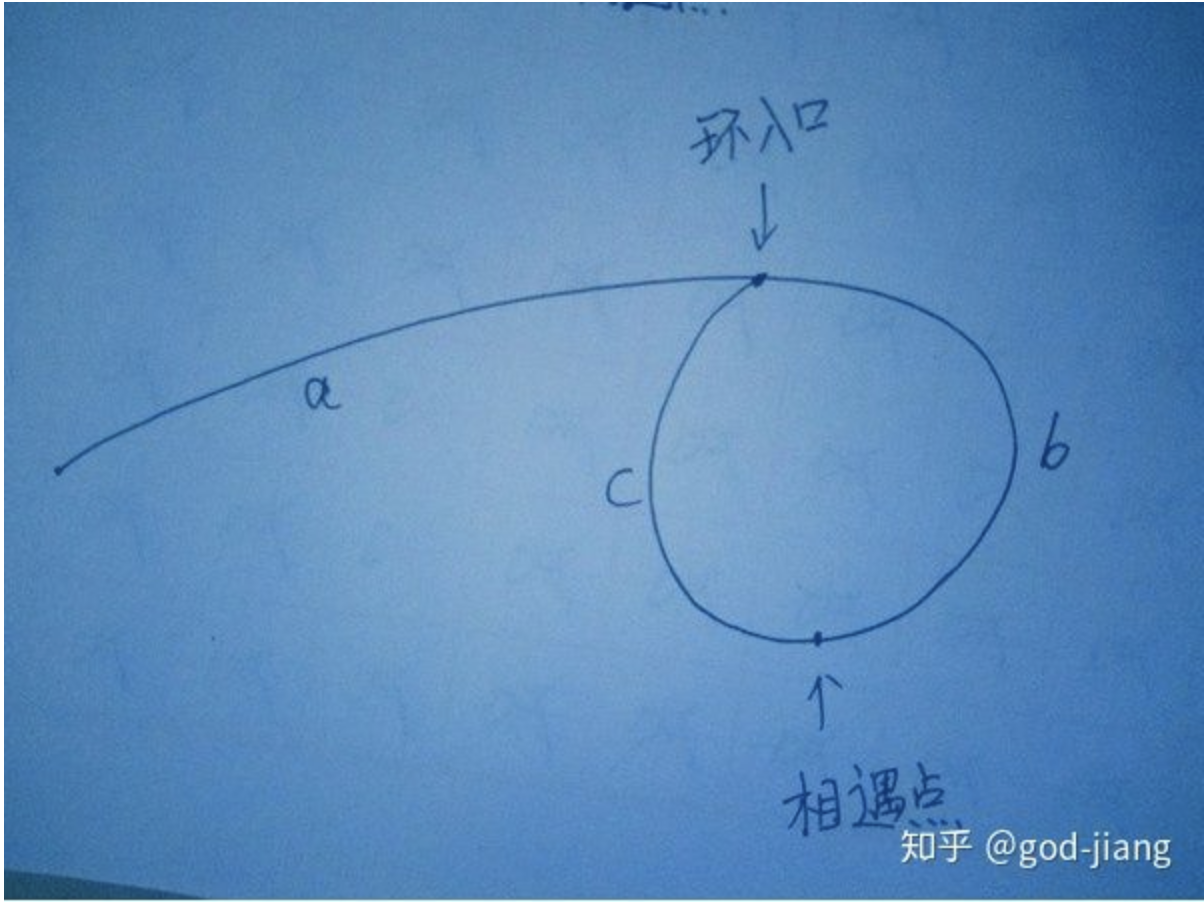
假设
链表头到环入口长度为——a,
环入口到相遇点长度为——b,
相遇点到环入口长度为——c,如图所示:
则相遇时,
快指针路程=a+(b+c)k+b,k>=1 ,其中b+c为环的长度,k为环的圈数(k>=1,即最少一圈,不能是0圈,不然快慢指针走的路程一样,矛盾)。
慢指针路程=a+b 。
因为快指针的路程是慢指针的路程的两倍,所以:(a+b)*2=a+(b+c)k+b 。
化简得:
a=(k-1)(b+c)+c ,这个式子的意思是:链表头到环入口的距离=相遇点到环入口的距离+(k-1)圈数环长度 。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发,最后一定相遇于环入口。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def EntryNodeOfLoop (self, pHead ): if pHead == None and pHead.next == None : return None onestep = pHead twostep = pHead while twostep and twostep.next : onestep = onestep.next twostep = twostep.next .next if onestep == twostep: onestep = pHead while onestep != twostep: onestep = onestep.next twostep = twostep.next return onestep return None
interview_56 解题思路:因为重复的节点都要删除,因此需要标记重复开始前的上一个节点,又因为头结点有可能是重复的节点,为了操作方便,我们可以再链表前面设置一个空节点作为头结点,因此需要设置3个指针,第一个head指向头结点。第二个p用来标记重复节点的前面一个节点,第三个cur用来寻找重复的节点,一旦找到p就不移动了,cur继续往后寻找直到不是重复的节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def deleteDuplication (self, pHead ): head = ListNode(-1 ) p = head p.next = pHead cur = pHead while cur and cur.next : if cur.val != cur.next .val: cur = cur.next p = p.next else : cur_val = cur.val while cur and cur.val == cur_val: cur = cur.next p.next = cur return head.next
BackTrack 回溯思想的模板为:
1 2 3 4 5 6 7 8 9 result = [] def backtrack (路径, 选择列表 ): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径, 选择列表) 撤销选择
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 import timeitclass Solution : def findMedianSortedArrays (self, nums1, nums2 ) -> float: m = len (nums1) n = len (nums2) k = (m + n) % 2 if k == 1 : return self.find_k(nums1, nums2, (m + n) // 2 ) else : return ( self.find_k(nums1, nums2, (m + n) // 2 - 1 ) + self.find_k(nums1, nums2, (m + n) // 2 ) ) / 2 def find_k (self, nums1, nums2, k ): if not nums1: return nums2[k] if not nums2: return nums1[k] i = len (nums1) // 2 j = len (nums2) // 2 if k > i + j: if nums1[i] > nums2[j]: return self.find_k(nums1, nums2[j + 1 :], k - j - 1 ) else : return self.find_k(nums1[i + 1 :], nums2, k - i - 1 ) else : if nums1[i] > nums2[j]: return self.find_k(nums1[:i], nums2, k) else : return self.find_k(nums1, nums2[:j], k) if __name__ == "__main__" : so = Solution() nums1 = [1 , 2 , 3 ] nums2 = [1 , 2 , 3 ] start = timeit.default_timer() print(so.findMedianSortedArrays(nums1, nums2)) end = timeit.default_timer() print(str ((end - start) * 1000 ), "s" ) nums1 = [1 , 2 , 3 ] nums2 = [4 , 5 , 6 ] print(so.findMedianSortedArrays(nums1, nums2)) nums1 = [1 , 2 , 3 ] nums2 = [4 , 5 ] print(so.findMedianSortedArrays(nums1, nums2)) nums1 = [1 , 4 , 6 ] nums2 = [2 , 5 ] print(so.findMedianSortedArrays(nums1, nums2))
sudoku-solver 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 from collections import defaultdictclass Solution : def solveSudoku (self, board ) -> None : rows_available = [set (range (1 , 10 )) for _ in range (9 )] columns_available = [set (range (1 , 10 )) for _ in range (9 )] boxes_available = [set (range (1 , 10 )) for _ in range (9 )] empty = [] for row in range (9 ): for column in range (9 ): if board[row][column] == "." : empty.append((row, column)) else : num = int (board[row][column]) rows_available[row].remove(num) columns_available[column].remove(num) boxes_available[(row // 3 ) * 3 + column // 3 ].remove(num) def backtrack (interation = 0 ): if interation == len (empty): return True i, j = empty[interation] for value in rows_available[i] & columns_available[j] & boxes_available[(i // 3 ) * 3 + j // 3 ]: rows_available[i].remove(value) columns_available[j].remove(value) boxes_available[(i // 3 ) * 3 + j // 3 ].remove(value) board[i][j] = value if backtrack(interation + 1 ): return True rows_available[i].add(value) columns_available[j].add(value) boxes_available[(i // 3 ) * 3 + j // 3 ].add(value) return False backtrack() return board so = Solution() print(so.solveSudoku([ ["5" , "3" , "." , "." , "7" , "." , "." , "." , "." ], ["6" , "." , "." , "1" , "9" , "5" , "." , "." , "." ], ["." , "9" , "8" , "." , "." , "." , "." , "6" , "." ], ["8" , "." , "." , "." , "6" , "." , "." , "." , "3" ], ["4" , "." , "." , "8" , "." , "3" , "." , "." , "1" ], ["7" , "." , "." , "." , "2" , "." , "." , "." , "6" ], ["." , "6" , "." , "." , "." , "." , "2" , "8" , "." ], ["." , "." , "." , "4" , "1" , "9" , "." , "." , "5" ], ["." , "." , "." , "." , "8" , "." , "." , "7" , "9" ] ] ))
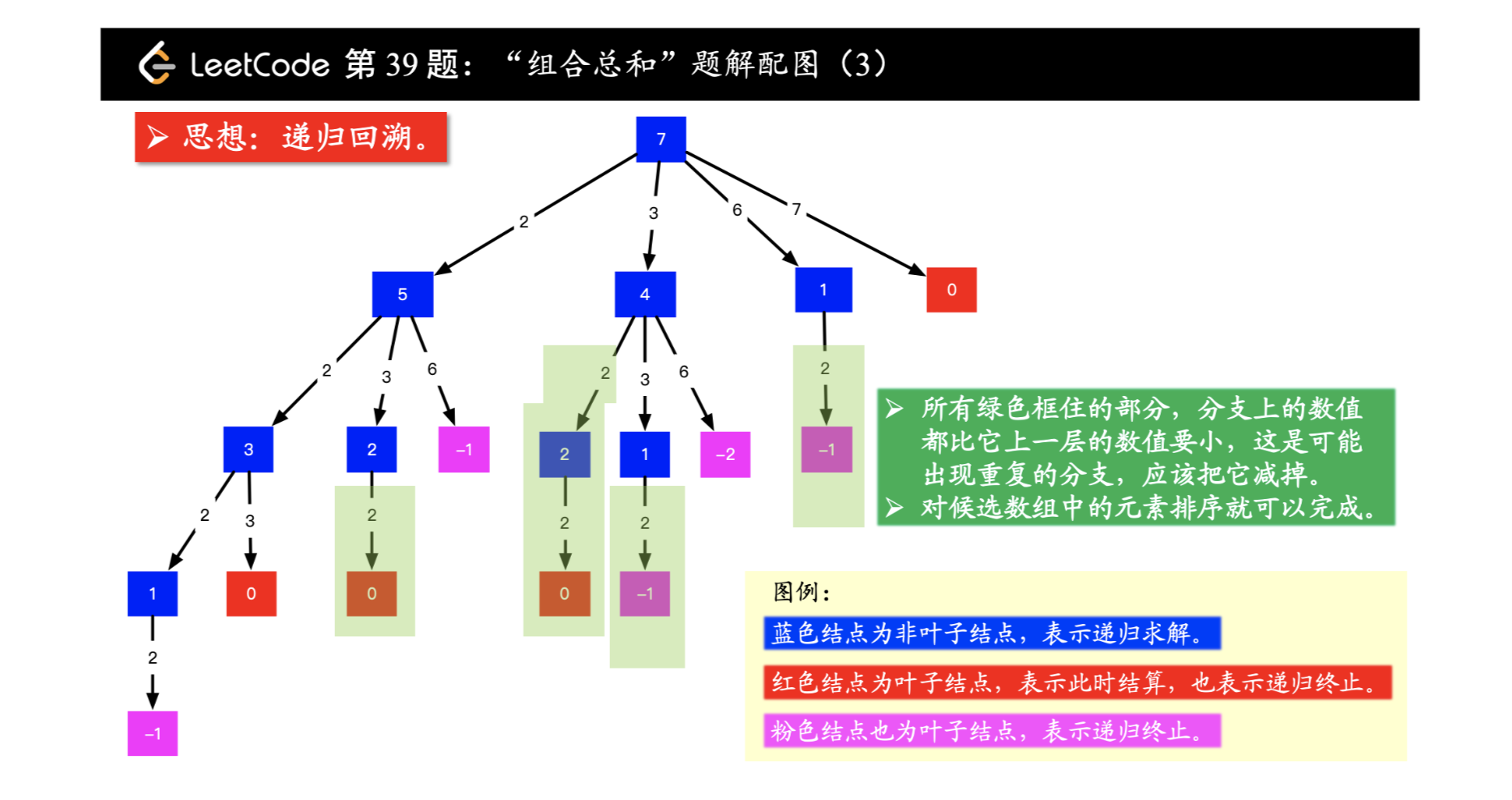
combination-sum 解题思路:(注:参考链接 )
以 target = 7 为根结点,每一个分支做减法。减到 00 或者负数的时候,剪枝。其中,减到 0的时候添加结果。
为了能够去重:把候选数组排个序,即后面选取的数不能比前面选的数还要小。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 from typing import Listclass Solution : def combinationSum (self, candidates: List[int ], target: int ) -> List[List[int]]: if not candidates or not target: return [] candidates.sort() output_list = [] path = [] begin = 0 size = len (candidates) self._dfs(candidates, begin, size, path, output_list, target) return output_list def _dfs (self, candidates, begin, size, path, output_list, target ): if target == 0 : output_list.append(path[:]) for index in range (begin, size): residue = target - candidates[index] if residue < 0 : break path.append(candidates[index]) self._dfs(candidates, index, size, path, output_list, residue) path.pop() if __name__ == '__main__' : candidates = [2 , 3 , 6 , 7 ] target = 7 solution = Solution() result = solution.combinationSum(candidates, target) print(result)
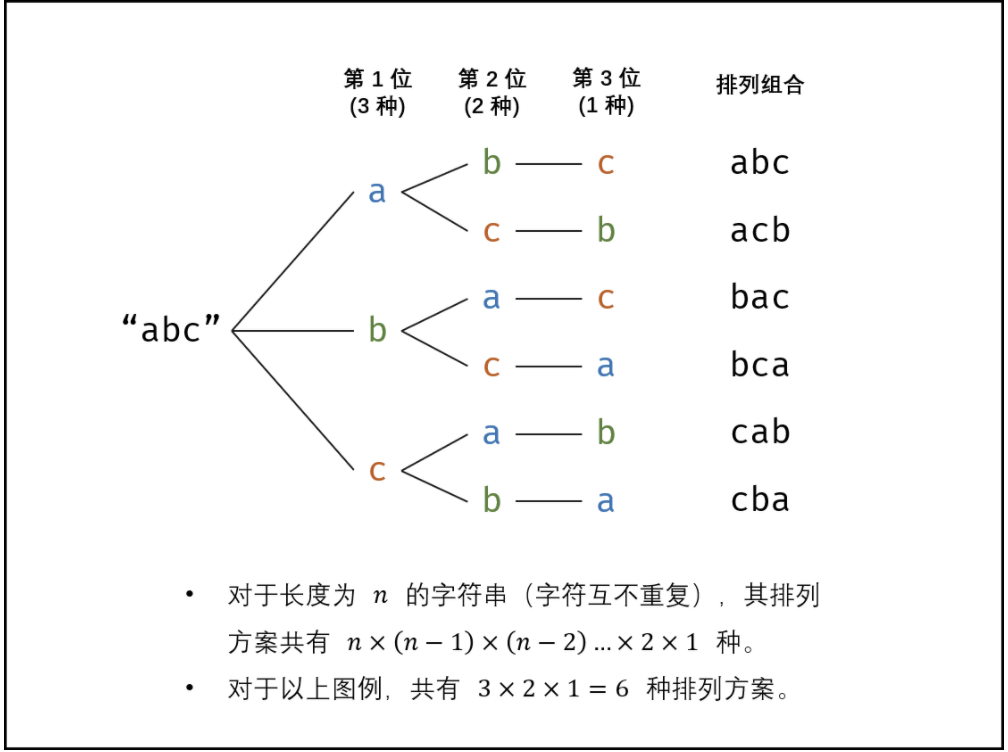
permutations
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def permute (self, nums ): def backtrack (nums, num ): if not nums: output_list.append(num) return for i in range (len (nums)): backtrack(nums[:i] + nums[i + 1 :], num + [nums[i]]) output_list = [] backtrack(nums, []) return output_list so = Solution() print(so.permute([1 , 2 , 3 ]))
permutations-ii 去除重复元素,两个要点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def permuteUnique (self, nums ): def backtrack (nums, num ): if not nums: output_list.append(num) return for i in range (len (nums)): if i > 0 and nums[i] == nums[i - 1 ]: continue backtrack(nums[:i] + nums[i + 1 :], num + [nums[i]]) nums.sort() output_list = [] backtrack(nums, []) return output_list so = Solution() print(so.permuteUnique([1 , 1 , 2 ]))
interview_27
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def permutation (self, s: str ) -> List[str]: if not s: return [] def backtrack (nums, tmp ): if not nums: result.add(tmp) return for i in range (len (nums)): backtrack(nums[:i] + nums[i+1 :], tmp+nums[i]) result = set () backtrack(s, "" ) return list (result) so = Solution() print(so.permutation("ryawrowv" ))
powx-n 解题思路
若n为偶数:$x^n = x^{\frac{n}{2}} \, \dot \, x^{\frac{n}{2}}$
若n为奇数:$x ^ n = x ^ {\frac{n}{2}} \, \dot \, x^ {\frac{n}{2}} \, \dot \, x$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def myPow (self, x: float , n: int ) -> float: if n == 0 : return 1 if n == -1 : return 1 / x half = self.myPow(x, n // 2 ) if n % 2 == 0 : return half * half else : return half * half * x so = Solution() print(so.myPow(2.00000 , -10 ))
n-queens 一、因为:
对于所有的主对角线有 行号 + 列号 = 常数
对于所有的次对角线有 行号 - 列号 = 常数
所以,所有的主对象线元素可以用2 * n - 1个元素来表示,比如main_diagonals[0]就可以表示待解queen_map中,第queen_map[0][0]个元素的所有 主对角线元素。
二、解题思路 (注:参考链接 )
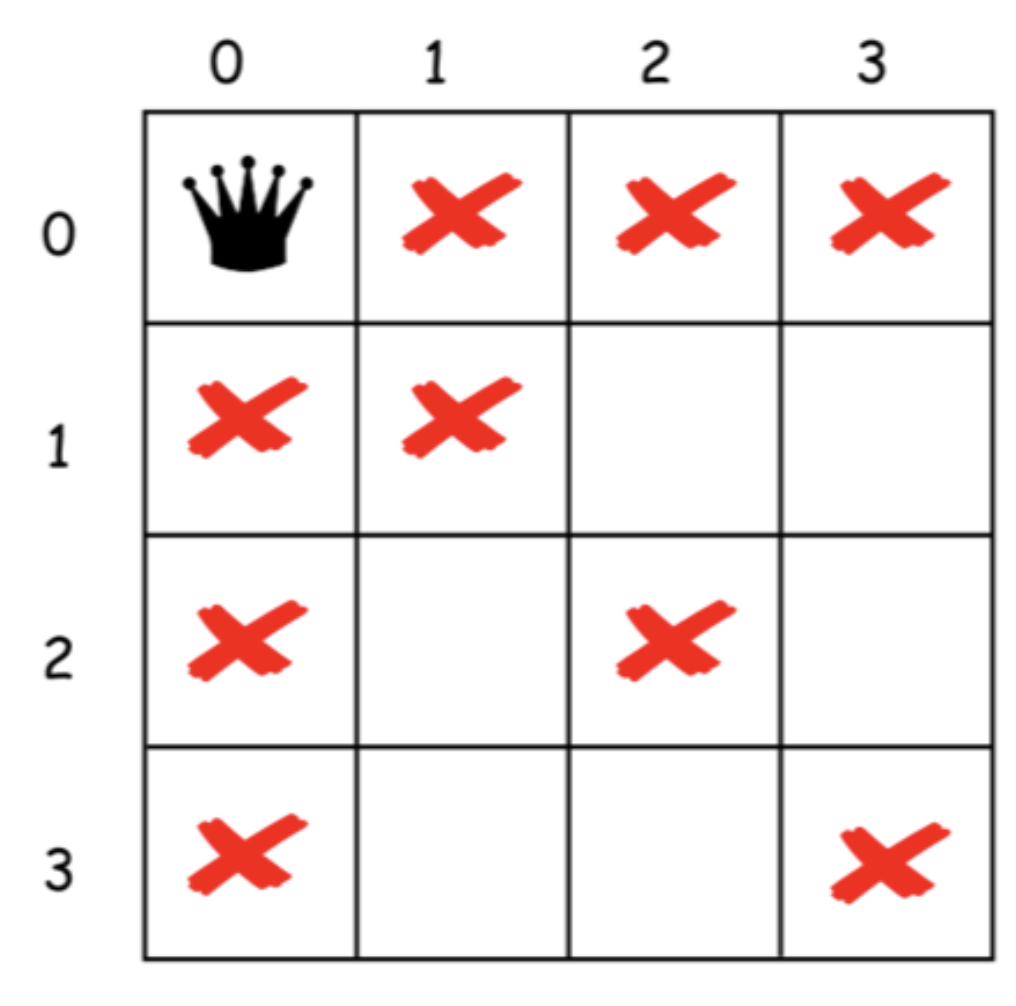
从第一个 row = 0 开始.
循环列并且试图在每个 column 中放置皇后.
如果方格 (row, column) 不在攻击范围内
在 (row, column) 方格上放置皇后。
排除对应行,列和两个对角线的位置。
If 所有的行被考虑过,row == N
Else
回溯:将在 (row, column) 方格的将皇后移除。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 from typing import Listclass Solution : def solveNQueens (self, n: int ) -> List[List[str]]: def could_place (row, col ): return not cols[col] + main_diagonals[row - col] + counter_diagonals[row + col] def place_queen (row, col ): queens_position.add((row, col)) cols[col] = 1 main_diagonals[row - col] = 1 counter_diagonals[row + col] = 1 def remove_queen (row, col ): queens_position.remove((row, col)) cols[col] = 0 main_diagonals[row - col] = 0 counter_diagonals[row + col] = 0 def add_solution (): solution = [] for _, col in sorted (queens_position): solution.append('.' * col + 'Q' + '.' * (n - col - 1 )) output.append(solution) def backtrack (row=0 ): for col in range (n): if could_place(row, col): place_queen(row, col) if row + 1 == n: add_solution() else : backtrack(row + 1 ) remove_queen(row, col) cols = [0 ] * n main_diagonals = [0 ] * (2 * n - 1 ) counter_diagonals = [0 ] * (2 * n - 1 ) queens_position = set () output = [] backtrack() return output so = Solution() print(so.solveNQueens(4 ))
n-queens-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 from typing import Listclass Solution : def totalNQueens (self, n: int ) -> int: def could_place (row, col ): return ( not cols[col] + main_diagonals[row - col] + counter_diagonals[row + col] ) def place_queen (row, col ): cols[col] = 1 main_diagonals[row - col] = 1 counter_diagonals[row + col] = 1 def remove_queen (row, col ): cols[col] = 0 main_diagonals[row - col] = 0 counter_diagonals[row + col] = 0 def backtrack (row=0 , output = 0 ): for col in range (n): if could_place(row, col): place_queen(row, col) if row + 1 == n: output += 1 else : output = backtrack(row + 1 , output) remove_queen(row, col) return output cols = [0 ] * n main_diagonals = [0 ] * (2 * n - 1 ) counter_diagonals = [0 ] * (2 * n - 1 ) return backtrack() so = Solution() print(so.totalNQueens(4 ))
combinations 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def combine (self, n: int , k: int ) -> List[List[int]]: if n <= 0 or k <= 0 or n < k: return [] result = [] self.__dfs(1 , k, n, [], result) return result def __dfs (self, index, k, n, pre, result ): if len (pre) == k: result.append(pre[:]) return for i in range (index, n + 1 ): pre.append(i) self.__dfs(i + 1 , k, n, pre, result) pre.pop() so = Solution() print(so.combine(4 , 2 ))
subsets 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from typing import Listclass Solution : def subsets (self, nums: List[int ] ) -> List[List[int]]: result = [] n = len (nums) if n <= 0 : return result def backtrack (start, result_tmp ): result.append(result_tmp) for i in range (start, n): backtrack(i + 1 , result_tmp + [nums[i]]) backtrack(0 , []) return result so = Solution() print(so.subsets([1 , 2 , 3 ]))
subsets-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 from typing import Listclass Solution : def subsetsWithDup (self, nums: List[int ] ) -> List[List[int]]: n = len (nums) nums.sort() def track_back (i, tmp ): res.append(tmp) for j in range (i, n): if j > i and nums[j] == nums[j - 1 ]: continue track_back(j + 1 , tmp + [nums[j]]) res = [] track_back(0 , []) return res so = Solution() print(so.subsetsWithDup([0 ]))
word-search 可以参考interview_65 写法更清楚明了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 from typing import Listclass Solution : derections = [(0 , -1 ), (-1 , 0 ), (0 , 1 ), (1 , 0 )] def exist (self, board: List[List[str ]], word: str ) -> bool: rows = len (board) cols = len (board[0 ]) marked = [[False for _ in range (cols)] for _ in range (rows)] for row in range (rows): for col in range (cols): if self.__search_word(board, word, 0 , row, col, marked, rows, cols): return True return False def __search_word (self, board, word, index_word, row, col, marked, rows, cols ): if len (word) - 1 == index_word: return board[row][col] == word[index_word] if board[row][col] == word[index_word]: marked[row][col] = True for derection in self.derections: next_x, next_y = row + derection[0 ], col + derection[1 ] if 0 <= next_x < rows and 0 <= next_y < cols and not marked[next_x][next_y] \ and self.__search_word(board, word, index_word + 1 , next_x, next_y, marked, rows, cols): return True marked[row][col] = False return False so = Solution() print(so.exist([ ['A' , 'B' , 'C' , 'E' ], ['S' , 'F' , 'C' , 'S' ], ['A' , 'D' , 'E' , 'E' ] ], "ABCCED" ))
interview_65 此题同word_search
对比参考链接 ,其方法更加简洁。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 from typing import Listclass Solution : def exist (self, board: List[List[str ]], word: str ) -> bool: def dfs (i, j, k ): if not 0 <= i < len (board) or not 0 <= j < len (board[0 ]) or word[k] != board[i][j] or board[i][j] == "*" : return False if k == len (word)-1 : return True tmp = board[i][j] board[i][j] = "*" result = dfs(i-1 , j, k+1 ) or dfs(i+1 , j, k+1 ) or dfs(i, j-1 , k+1 ) or dfs(i, j+1 , k+1 ) board[i][j] = tmp return result for i in range (len (board)): for j in range (len (board[0 ])): if dfs(i, j, 0 ): return True return False
牛客网上的要求略有不同。
给出的是字符串,需要将matrix[row][col]写成matrix[row*cols+col]来定位
字符串是不可变变量,需要将matrix先转化为list(matrix)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def hasPath (self, matrix, rows, cols, path ): def dfs (row, col, k ): if not 0 <= row < rows or not 0 <= col < cols or k >= len (path) or path[k] != matrix[row*cols + col] or matrix[row*cols + col] == "*" : return False if matrix[row*cols + col] == path[k] and k == len (path) - 1 : return True tmp = matrix[row*cols + col] matrix[row*cols + col] = "*" if dfs(row+1 , col, k+1 ) or dfs(row, col+1 , k+1 ) or dfs(row-1 , col, k+1 ) or dfs(row, col-1 , k+1 ): matrix[row*cols + col] = tmp return True matrix[row*cols + col] = tmp return False matrix = list (matrix) for row in range (rows): for col in range (cols): if dfs(row, col, 0 ): return True return False
interview_66 参考链接
广度优先搜索:一般使用队列 来实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from collections import dequeclass Solution : def movingCount_BFS (self, m: int , n: int , k: int ) -> int: def sum_step (row, col ): result = 0 while row > 0 : result += row % 10 row = row // 10 while col > 0 : result += col % 10 col = col // 10 return result de = deque() de.append((0 , 0 )) marked = set () while de: x, y = de.popleft() if (x, y) not in marked and sum_step(x, y) <= k: marked.add((x, y)) for dx, dy in [(1 , 0 ), (0 , 1 )]: if x + dx < m and y + dy < n: de.append((x+dx, y+dy)) return len (marked)
深度优先搜索:一般使用栈 来实现
定义一个递归函数 dfs(),如果坐标不满足条件,结束递归状态,否则将下一步满足条件的坐标代入递归函数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution : def movingCount (self, m: int , n: int , k: int ) -> int: def sum_step (row, col ): result = 0 while row > 0 : result += row % 10 row = row // 10 while col > 0 : result += col % 10 col = col // 10 return result def dfs (x, y ): if x >= m or y >= n or sum_step(x, y) > k or (x, y) in marked: return marked.add((x, y)) dfs(x + 1 , y) dfs(x, y + 1 ) marked = set () dfs(0 , 0 ) return len (marked)
restore-ip-addresses 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def restoreIpAddresses (self, s: str ) -> List[str]: r = [] def restore (count=0 , ip='' , s='' ): if count == 4 : if s == '' : r.append(ip[:-1 ]) return if len (s) > 0 : restore(count+1 , ip+s[0 ]+'.' , s[1 :]) if len (s) > 1 and s[0 ] != '0' : restore(count+1 , ip+s[:2 ]+'.' , s[2 :]) if len (s) > 2 and s[0 ] != '0' and int (s[0 :3 ]) < 256 : restore(count+1 , ip+s[:3 ]+'.' , s[3 :]) restore(0 , '' , s) return r so = Solution() print(so.restoreIpAddresses("25525511135" ))
scramble-string 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 import functoolsclass Solution : @functools.lru_cache(None def isScramble (self, s1: str , s2: str ) -> bool: if len (s1) != len (s2): return False if s1 == s2: return True if sorted (s1) != sorted (s2): return False for i in range (1 , len (s1)): if self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:]): return True if self.isScramble(s1[:i], s2[-i:]) and self.isScramble(s1[i:], s2[:-i]): return True return False so = Solution() print(so.isScramble("great" , "rgtae" ))
different-ways-to-add-parentheses 分治三步法:
分解:按运算符分成左右两部分,分别求解
解决:实现一个递归函数,输入算式,返回算式解
合并:根据运算符合并左右两部分的解,得出最终解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 from typing import Listclass Solution : def diffWaysToCompute (self, input : str ) -> List[int]: if input .isdigit(): return [int (input )] res = [] for index, value in enumerate (input ): if value in ["+" , "-" , "*" ]: left = self.diffWaysToCompute(input [:index]) right = self.diffWaysToCompute(input [index + 1 :]) for l in left: for r in right: if value == "+" : res.append(l + r) elif value == "-" : res.append(l - r) elif value == "*" : res.append(l * r) return res so = Solution() print(so.diffWaysToCompute("2*3-4*5" ))
letter-case-permutation 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 from typing import Listclass Solution : def letterCasePermutation (self, S: str ) -> List[str]: result = [] def helper (s, pre ): if not s: result.append("" .join(pre)) return if s[0 ].isalpha(): helper(s[1 :], pre + [s[0 ].upper()]) helper(s[1 :], pre + [s[0 ].lower()]) else : helper(s[1 :], pre + [s[0 ]]) helper(S, []) return result so = Solution() print(so.letterCasePermutation("a1b2" ))
palindrome-partitioning 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from typing import Listclass Solution : def partition (self, s: str ) -> List[List[str]]: result = [] def backtrack (s, tmp ): if not s: result.append(tmp) return for i in range (1 , len (s) + 1 ): if s[:i] == s[:i][::-1 ]: backtrack(s[i:], tmp + [s[:i]]) backtrack(s, []) return result so = Solution() print(so.partition("aab" ))
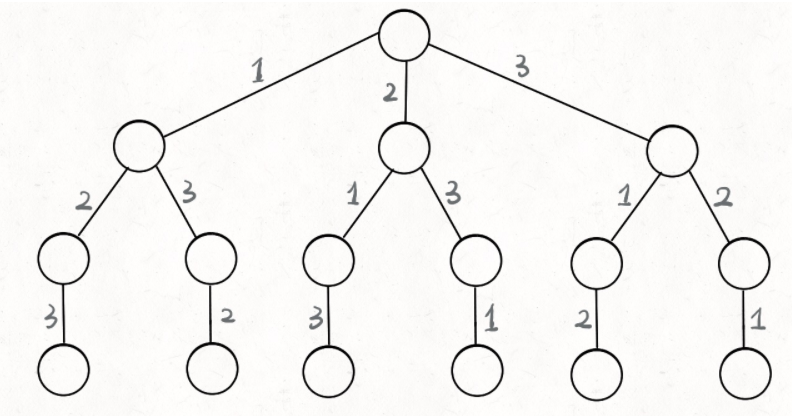
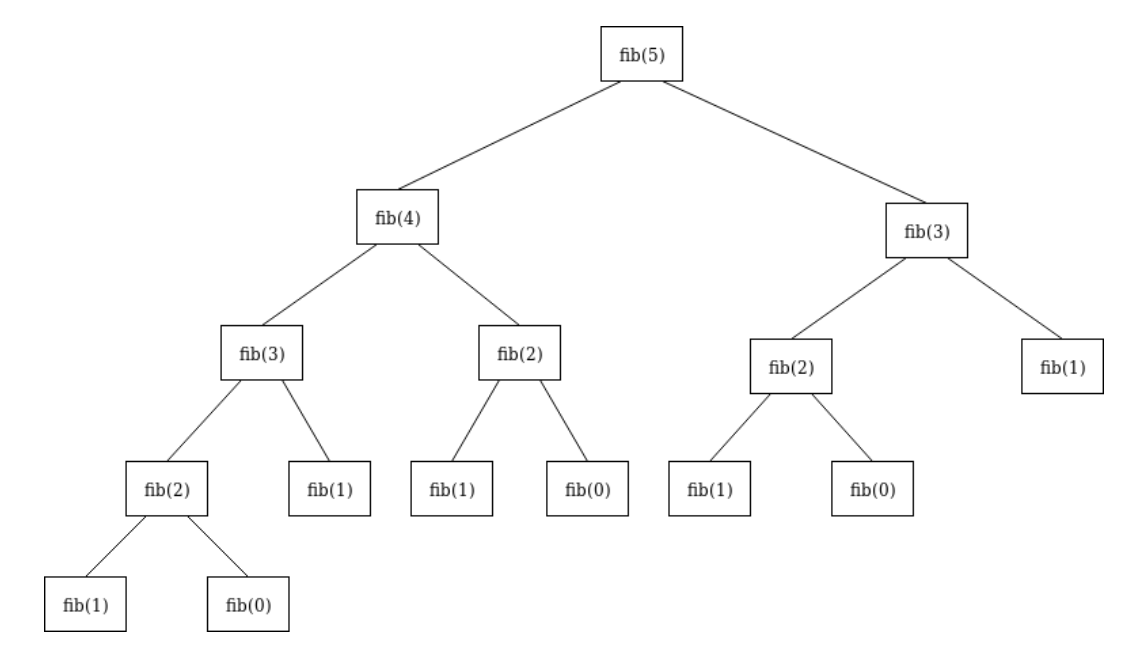
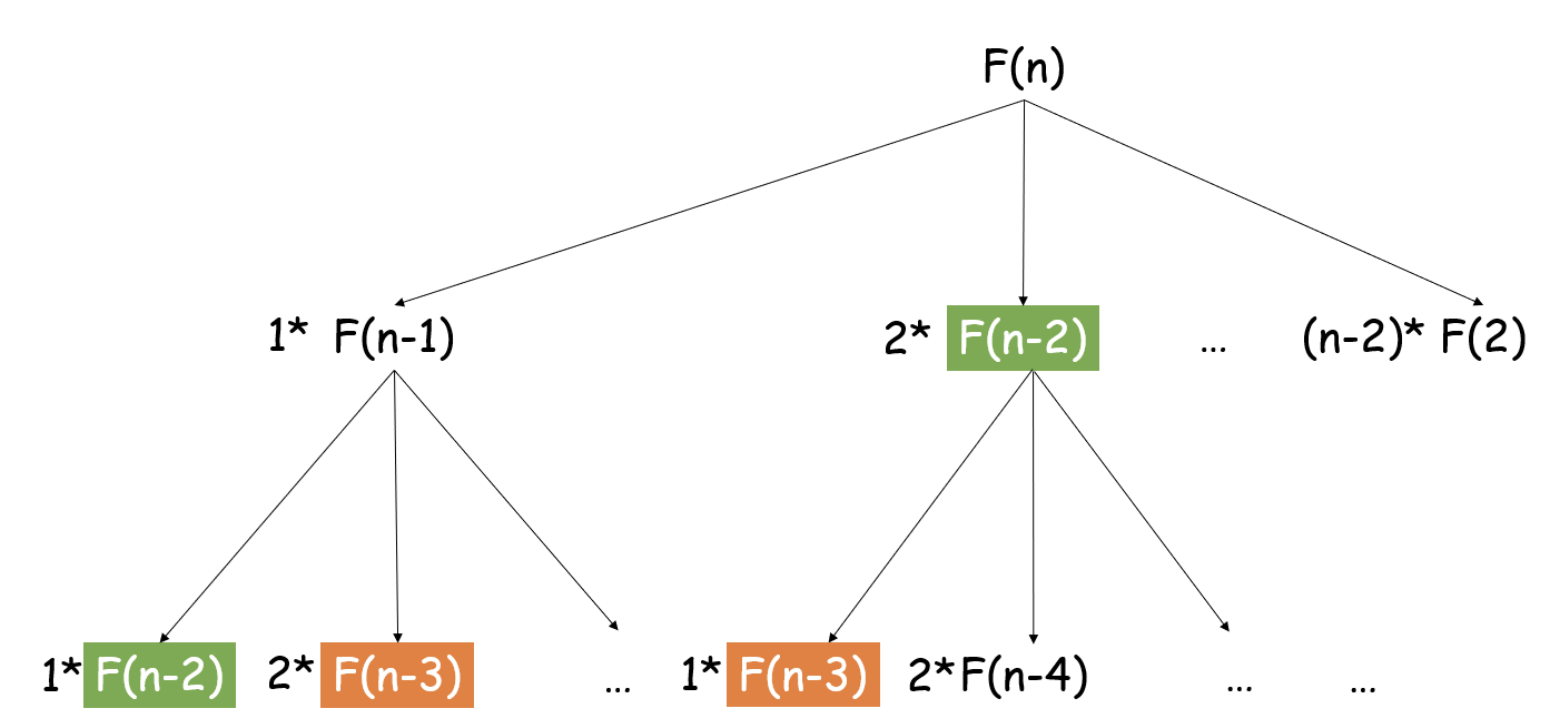
fibonacci-number 方法一:递归(递归树如下)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def fib (self, N: int ) -> int: if N == 0 : return 0 if N == 1 : return 1 return self.fib(N-1 ) + self.fib(N-2 ) so = Solution() print(so.fib(5 ))
递归虽然有简洁的优点,但是递归是函数调用自身,而函数调用是有时间和空间消耗的,每一次函数调用,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,而往栈里压入数据和弹出数据都需要时间。另外,递归中有可能很多计算都是重复的,从而也会对性能产生影响。
方法二:记忆化自底向上的方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def fib (self, N: int ) -> int: if N <= 1 : return N f_dict = {0 : 0 , 1 : 1 } for i in range (2 , N): f_dict[i] = f_dict[i - 1 ] + f_dict[i - 2 ] return f_dict[N - 1 ] so = Solution() print(so.fib(4 ))
Interview_10 解题思路:
类似于青蛙跳台阶,当n=1时,只有一种横向排列的方式。
当n等于二时,2*2有两种选择,横向或者是竖向。
当n等于3的时候对于2*3来说,如果选择的是竖向排列,则剩下的就是2*2排列。
如果选择的是横向,则对于2*n剩下的则只有1*n的一种选择。
2*n的大矩形就相当于“跳台阶“问题中的台阶,大矩形的长度n相当于台阶的个数n;从左至右的去覆盖,把小矩形竖着放相当于跳一个台阶,把小矩阵横着放相当于跳两个台阶 。故:当前n的覆盖种数 = 当前n-1的覆盖总数 + 当前n-2的覆盖总数。即:f (n) = f (n-1) + f (n-2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def rectCover (self, number ): if number == 1 : return 1 elif number == 2 : return 2 return self.rectCover(number-1 ) + self.rectCover(number-2 ) so = Solution() print(so.rectCover(3 ))
或着使用自底向上的方法,节省空间
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def rectCover (self, number ): if number <= 2 : return number dp = [0 for _ in range (number)] dp[0 ] = 1 dp[1 ] = 2 for i in range (2 , number): dp[i] = dp[i-1 ] + dp[i-2 ] return dp[-1 ]
2DMatric 5_longest_palindrome 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution : def longestPalindrome (self, s: str ) -> str: longest_str = "" longestLen = 0 matrics = [[0 for i in range (0 , len (s))] for i in range (0 , len (s))] for j in range (0 , len (s)): for i in range (0 , j + 1 ): if j - i <= 1 : if s[i] == s[j]: matrics[i][j] = 1 if longestLen < j - i + 1 : longestLen = j - i + 1 longest_str = s[i : j + 1 ] else : if s[i] == s[j] and matrics[i + 1 ][j - 1 ]: matrics[i][j] = 1 if longestLen < j - i + 1 : longestLen = j - i + 1 longest_str = s[i : j + 1 ] return longest_str s = "abccba" so = Solution() print(so.longestPalindrome(s))
rotate-image 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution : def ero_matrics (self, matric ): if not matric: return matric for i in range (0 , len (matric)): for j in range (i, len (matric)): tmp = matric[i][j] matric[i][j] = matric[j][i] matric[j][i] = tmp for i in range (0 , len (matric)): for j in range (0 , len (matric) // 2 ): tmp = matric[i][j] matric[i][j] = matric[i][len (matric) - j - 1 ] matric[i][len (matric) - j - 1 ] = tmp return matric so = Solution() print(so.ero_matrics([[4 , 8 , 12 , 16 ], [3 , 7 , 11 , 15 ], [2 , 6 , 10 , 14 ], [1 , 5 , 9 , 13 ]])) print(so.ero_matrics([ [3 , 6 , 9 ], [2 , 5 , 8 ], [1 , 4 , 7 ]]))
spiral-matrix 解题思路来源于leetcode官网:按层模拟(注:参考链接 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 from typing import Listclass Solution : def spiralOrder (self, matrix: List[List[int ]] ) -> List[int]: def spiral_matrix (r1, c1, r2, c2 ): for c in range (c1, c2 + 1 ): yield r1, c for r in range (r1 + 1 , r2 + 1 ): yield r, c2 if r1 < r2 and c1 < c2: for c in range (c2 - 1 , c1, -1 ): yield r2, c for r in range (r2, r1, -1 ): yield r, c1 if not matrix: return [] output = [] r1, r2 = 0 , len (matrix) - 1 c1, c2 = 0 , len (matrix[0 ]) - 1 while r1 <= r2 and c1 <= c2: for r, c in spiral_matrix(r1, c1, r2, c2): output.append(matrix[r][c]) r1 += 1 r2 -= 1 c1 += 1 c2 -= 1 return output so = Solution() print(so.spiralOrder([ [1 , 2 , 3 ], [4 , 5 , 6 ], [7 , 8 , 9 ] ]))
spiral-matrix-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 from typing import Listclass Solution : def generateMatrix (self, n: int ) -> List[List[int]]: if n < 1 : return [] def spiral_matrix (r1, c1, r2, c2 ): for c in range (c1, c2 + 1 ): yield r1, c for r in range (r1 + 1 , r2 + 1 ): yield r, c2 if r1 < r2 and c1 < c2: for c in range (c2 - 1 , c1, -1 ): yield r2, c for r in range (r2, r1, -1 ): yield r, c1 output_matrix = [[0 for i in range (n)] for i in range (n)] r1, r2 = 0 , len (output_matrix) - 1 c1, c2 = 0 , len (output_matrix[0 ]) - 1 number = 1 while r1 <= r2 and c1 <= c2: for r, c in spiral_matrix(r1, c1, r2, c2): output_matrix[r][c] = number number += 1 r1 += 1 r2 -= 1 c1 += 1 c2 -= 1 return output_matrix so = Solution() print(so.generateMatrix(3 ))
set-matrix-zeroes 解题思路如下:
matrics第一行与第一列用于存储对应行或列是否有0
flag用于存储第一行或者第一列是否存在0
首先遍历第一行与第一列是否存在0,若存在将flag置为0
再遍历其他行,若存在0,将相应第一行和第一列的元素置为0
再次遍历第一行与第一列,将0所在的行和列中的所有元素置为0
最后,若flag为0,则把第一行和第一列的所有元素置为0。否则直接退出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from typing import Listclass Solution : def setZeroes (self, matrix: List[List[int ]] ) -> List: """ Do not return anything, modify matrix in-place instead. """ flag_col = False rows = len (matrix) cols = len (matrix[0 ]) for row in range (rows): if matrix[row][0 ] == 0 : flag_col = True for col in range (1 , cols): if matrix[row][col] == 0 : matrix[row][0 ] = matrix[0 ][col] = 0 for row in range (rows - 1 , -1 , -1 ): for col in range (cols - 1 , 0 , -1 ): if matrix[row][0 ] == 0 or matrix[0 ][col] == 0 : matrix[row][col] = 0 if flag_col: matrix[row][0 ] = 0 return matrix so = Solution() print(so.setZeroes([ [0 , 1 , 2 , 0 ], [3 , 4 , 5 , 2 ], [1 , 3 , 1 , 5 ] ]))
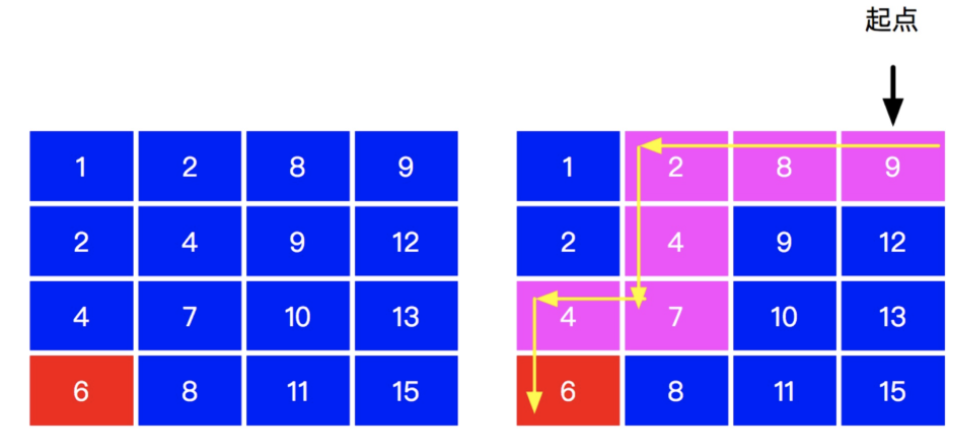
interview_1 如果从左上角开始找,“从上到下”和“从左到右”,遇到的数字都是逐渐增大的;
如果从右下角开始找,“从下到上”和“从右到左”,遇到的数字都是逐渐减小的;
所以,可以从左下或者右上开始搜索,以保证不走“回头路”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 from typing import Listclass Solution : def findNumberIn2DArray (self, matrix: List[List[int ]], target: int ) -> bool: if not matrix or target is None : return False rows = len (matrix) cols = len (matrix[0 ]) if rows == 0 or cols == 0 : return False x = 0 y = cols - 1 while x < rows and y >= 0 : if matrix[x][y] == target: return True if matrix[x][y] > target: y -= 1 else : x += 1 return False so = Solution() print(so.findNumberIn2DArray([ [1 , 4 , 7 , 11 , 15 ], [2 , 5 , 8 , 12 , 19 ], [3 , 6 , 9 , 16 , 22 ], [10 , 13 , 14 , 17 , 24 ], [18 , 21 , 23 , 26 , 30 ] ], 21 ))
interview_19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 from typing import Listclass Solution : def spiralOrder (self, matrix: List[List[int ]] ) -> List[int]: def spiral_matrix (r1, c1, r2, c2 ): for c in range (c1, c2 + 1 ): yield r1, c for r in range (r1 + 1 , r2 + 1 ): yield r, c2 if r1 < r2 and c1 < c2: for c in range (c2 - 1 , c1, -1 ): yield r2, c for r in range (r2, r1, -1 ): yield r, c1 if not matrix: return [] output = [] r1, r2 = 0 , len (matrix) - 1 c1, c2 = 0 , len (matrix[0 ]) - 1 while r1 <= r2 and c1 <= c2: for r, c in spiral_matrix(r1, c1, r2, c2): output.append(matrix[r][c]) r1 += 1 r2 -= 1 c1 += 1 c2 -= 1 return output so = Solution() print(so.spiralOrder([[1 , 2 , 3 ], [4 , 5 , 6 ], [7 , 8 , 9 ]]))
interview_51 参考链接
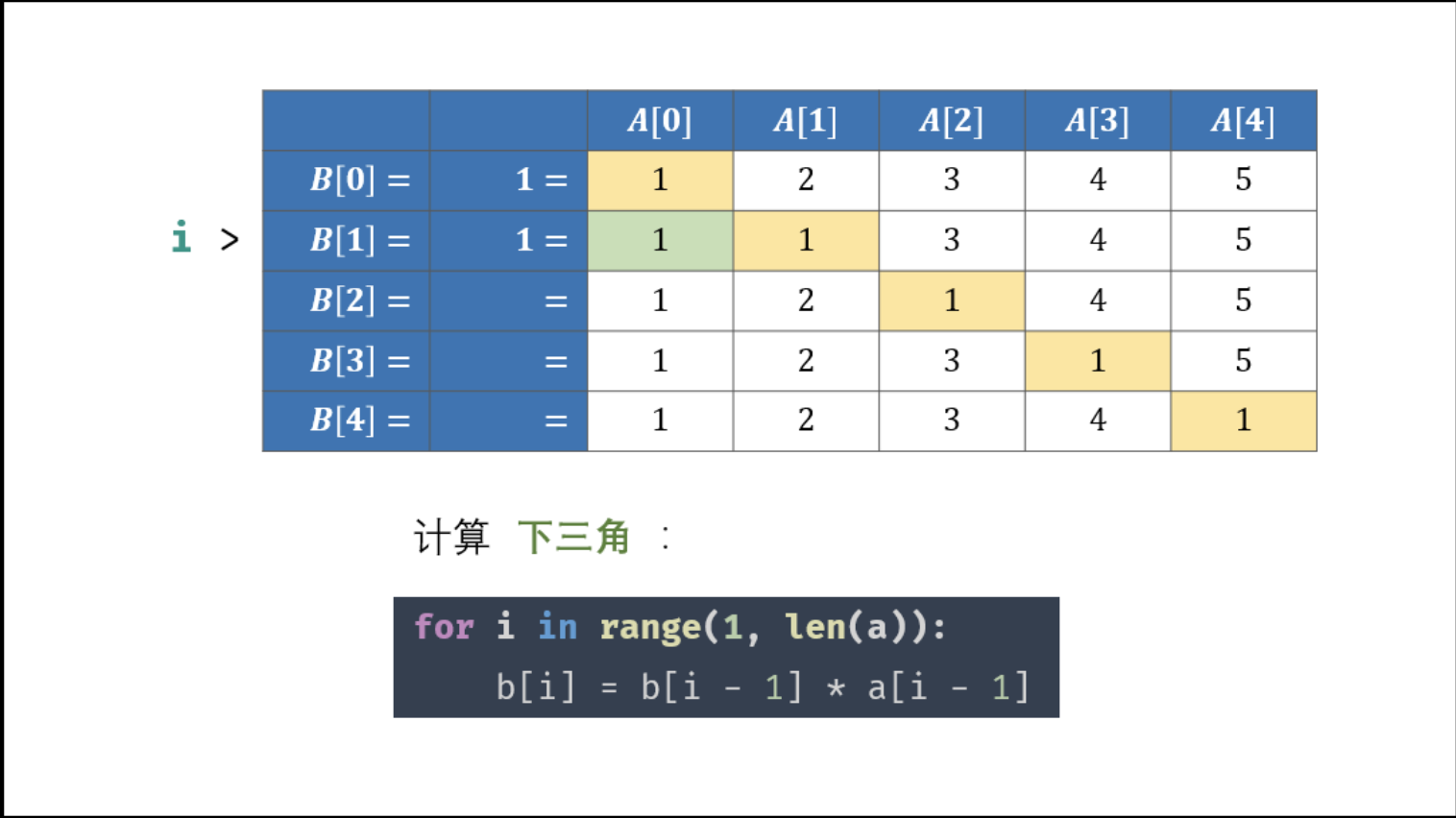
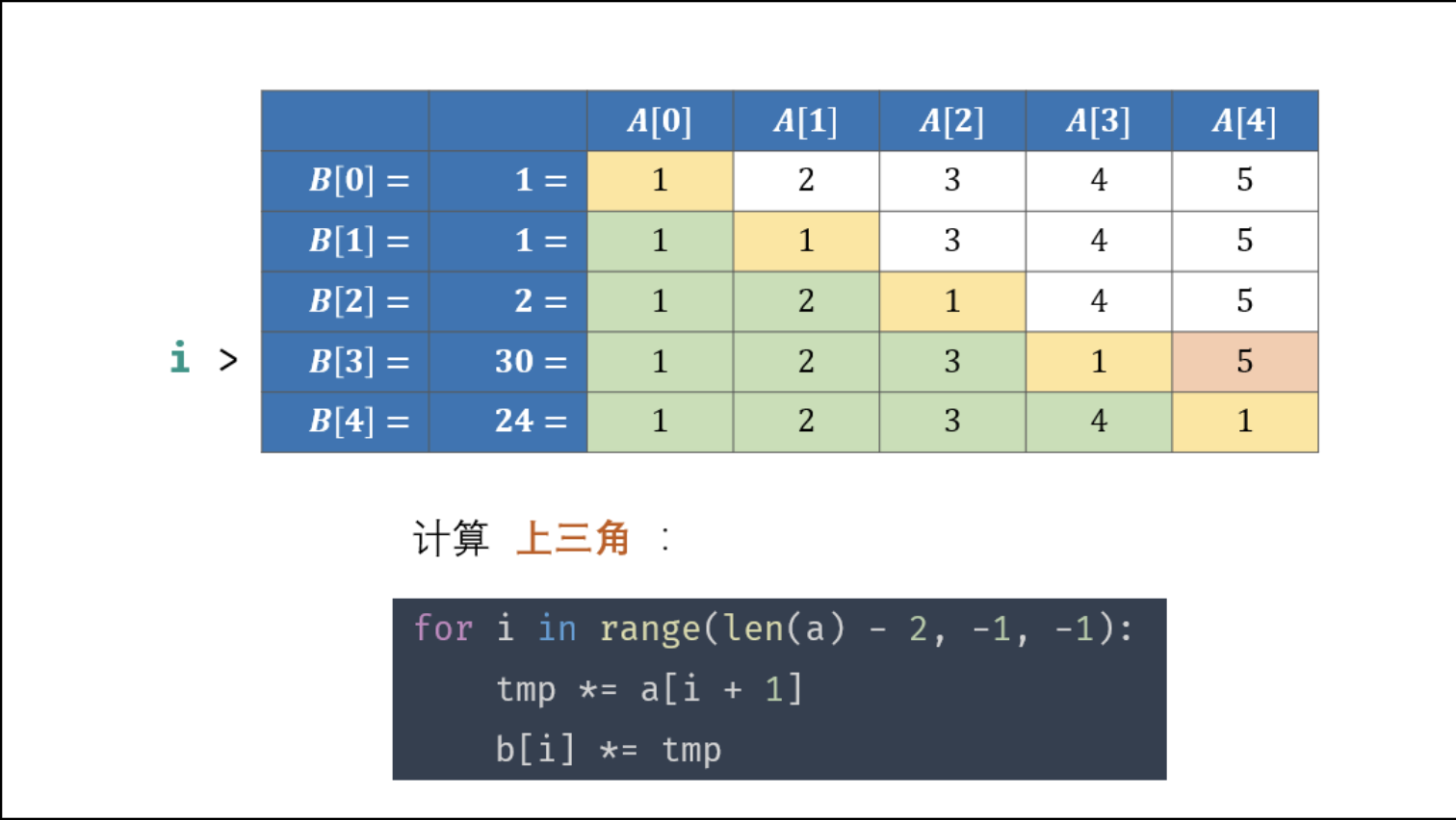
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 from typing import Listclass Solution : def constructArr (self, a: List[int ] ) -> List[int]: b, tmp = [1 ] * len (a), 1 for i in range (1 , len (a)): b[i] = b[i - 1 ] * a[i - 1 ] for i in range (len (a) - 2 , -1 , -1 ): tmp *= a[i + 1 ] b[i] *= tmp return b so = Solution() print(so.constructArr([1 , 2 , 3 , 4 , 5 ]))
interview_35 方法一:暴力法
时间复杂度$O(n^2)$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from typing import Listclass Solution : def reversePairs (self, nums: List[int ] ) -> int: if not nums: return 0 len_nums = len (nums) if len_nums <= 1 : return 0 result = 0 for i in range (len_nums): for j in range (i + 1 , len_nums): if nums[j] < nums[i]: result += 1 return result so = Solution() print(so.reversePairs([7 , 5 , 6 , 4 ]))
方法二:归并排序
解题思路
归并排序的时间复杂度是$O(NlogN)$
首先复习下归并排序:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 """ 用于分解 """ def mergeSort (nums ): len_nums = len (nums) if len_nums <= 1 : return nums mid = len_nums // 2 nums1 = mergeSort(nums[:mid]) nums2 = mergeSort(nums[mid:] return merge(nums1, nums2) """ 用于合并:将产生一个排好序的数组 """ def merge (nums1, nums2 ): sum_nums = [] i, j = 0 , 0 while i < len (nums1) and j < len (nums2): if nums1[i] <= nums2[j]: sum_nums.append(nums1[i]) i += 1 else : sum_nums.append(nums2[j]) j += 1 sum_nums += nums1[i:] sum_nums += nums2[j:] return sum_nums
在合并部分,归并是利用一个sum_nums逐个将较小 的元素添加至尾部,从而得到一个顺序数组。如果现在要从数组尾部开始遍历,同样产生一个顺序数组 ,要怎么做呢。
可以看到,改动点只是在merge函数里,将两个列表每次比较后较大的元素,从后往前的添加到sum_nums里即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 """ 用于分解 """ def mergeSort (nums ): len_nums = len (nums) if len_nums <= 1 : return nums mid = len_nums // 2 nums1 = mergeSort(nums[:mid]) nums2 = mergeSort(nums[mid:] return merge(nums1, nums2) """ 用于合并:将产生一个排好序的数组 """ def merge (nums1, nums2 ): i, j = len (nums1) - 1 , len (nums2) - 1 sum_nums = [0 ] * (i + j + 2 ) sum_nums_index = len (sum_nums) - 1 while i >= 0 and j >= 0 : if nums1[i] > nums2[j]: sum_nums[sum_nums_index] = nums1[i] i -= 1 sum_nums_index -= 1 else : sum_nums[sum_nums_index] = nums2[j] j -= 1 sum_nums_index -= 1 while i >= 0 : sum_nums[sum_nums_index] = nums1[i] i -= 1 sum_nums_index -= 1 while j >= 0 : sum_nums[sum_nums_index] = nums2[j] j -= 1 sum_nums_index -= 1 return sum_num mergeSort(nums)
现在应该一目了然了,接下来只要增加一个变量,将每次合并过程中的逆序对进行统计就可以了。因为在每次的合并过程中,nums1与nums2都是有序的,且 i,j分别指向两个数组。假如:
nums1 = [3, 6] nums2 = [2, 4]
对于6而言,6小于4( nums1[ i ] < nums2[ j ] ),构成一对逆序数。又因为两个数组都是有序的,所以我们知道,6大于nums2里 j 指向的当前最大的元素4,当然也会大于比4小的2。所以对于6而言,它能构成的逆序数对为 j + 1 == 2。( j = 0,……, len(nums2) - 1)
可以这样想,sum_nums只是保存了当前数组里的大小关系,这种顺序关系是为了便于逆序对个数的快速计算,它并没有改变原数组的顺序。
完整代码如下:利用全局变量count来记录合并过程中逆序对的个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 from typing import Listclass Solution : def __init__ (self ): self.count = 0 def reversePairs (self, nums: List[int ] ) -> int: """ 用于分解 """ def mergeSort (nums ): len_nums = len (nums) if len_nums <= 1 : return nums mid = len_nums // 2 nums1 = mergeSort(nums[:mid]) nums2 = mergeSort(nums[mid:]) return merge(nums1, nums2) """ 用于合并:将产生一个排好序的数组 """ def merge (nums1, nums2 ): i, j = len (nums1) - 1 , len (nums2) - 1 sum_nums = [0 ] * (i + j + 2 ) sum_nums_index = len (sum_nums) - 1 while i >= 0 and j >= 0 : if nums1[i] > nums2[j]: self.count += (j + 1 ) sum_nums[sum_nums_index] = nums1[i] i -= 1 sum_nums_index -= 1 else : sum_nums[sum_nums_index] = nums2[j] j -= 1 sum_nums_index -= 1 while i >= 0 : sum_nums[sum_nums_index] = nums1[i] i -= 1 sum_nums_index -= 1 while j >= 0 : sum_nums[sum_nums_index] = nums2[j] j -= 1 sum_nums_index -= 1 return sum_nums mergeSort(nums) return self.count so = Solution() print(so.reversePairs([1 , 3 , 2 , 3 , 1 ]))
Regular Expression string-to-integer-atoi 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 import reclass Solution : def myAtoi (self, s: str ) -> int: s = s.strip() if len (s) > 0 : pattern = r"[+-]?\d+" number = re.match(pattern, s) if number: number = int (number[0 ]) if number < -pow (2 , 31 ): return int (-pow (2 , 31 )) elif number > pow (2 , 31 ) - 1 : return int (pow (2 , 31 ) - 1 ) return number return 0 so = Solution() print(so.myAtoi("+123" ))
10_regular-expression-matchin 方法一:暴力求解, offer再见法
1 2 3 4 5 import reclass Solution : def isMatch (self, s: str , p: str ) -> bool: return (re.fullmatch(p, s) != None )
方法二:回溯求解
参考链接
首先,考虑只有“.”的情况。这种情况下只需要从左到右依次判断s[i]与p[i]是否匹配即可。
1 2 3 4 5 6 7 8 class Solution (object def isMatch (self, s: str , p: str ) -> bool: if not p: return not s first_match = s and (s[0 ] == p[0 ] or p[0 ] == "." ) return first_match and self.isMatch(s[1 :], p[1 :])
如果有“*”,它会出现在p[1]的位置,这时有两种情况:
“”匹配了0次前面的元素:这时直接比较”\ ”后面的元素即可。如“##”与“a*##”,即self.isMatch(s, p[2:])
“”匹配了1次或多次前面的元素:这时忽略s的第一个元素,继续与p进行比较。如“aaab”与“a\ b”,继续比较“aab”与“a*b”,可以理解为逐步走到了第一种情况。即self.isMatch(s[1:], p)
1 2 3 if len (p) > 2 and p[1 ] == "*" : return self.isMatch(s, p[2 :]) or \ (first_match and self.isMatch(s[1 :], p))
完整代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution (object def isMatch (self, s: str , p: str ) -> bool: if not p: return not s first_match = s and (s[0 ] == p[0 ] or p[0 ] == "." ) if len (p) >= 2 and p[1 ] == '*' : return self.isMatch(s, p[2 :]) or \ (first_match and self.isMatch(s[1 :], p)) else : return first_match and self.isMatch(s[1 :], p[1 :]) so = Solution() assert so.isMatch("mississippi" , "mis*is*ip*." )
方法三:动态规划
参考链接
interview_52 同regular-expression-matchin
valid-number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import reclass Solution : def isNumber (self, s: str ) -> bool: s = s.strip() if not s: return False if s[0 ] in ["+" , "-" ]: s = s[1 :] if "e" in s: s_list = s.split("e" ) if len (s_list) > 2 : return False s_list[0 ] = s_list[0 ].replace("." , "" , 1 ) if len (s_list[1 ]) > 0 and s_list[1 ][0 ] in ["+" , "-" ]: s_list[1 ] = s_list[1 ].replace(s_list[1 ][0 ], "" , 1 ) if s_list[0 ].isnumeric() and s_list[1 ].isnumeric(): return True else : s = s.replace("." , "" , 1 ) if s.isnumeric(): return True return False so = Solution() print(so.isNumber("53.5e93" ))
interview_53 解法一:暴力法(面试慎用)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import reclass Solution : def isNumber (self, s: str ) -> bool: if not s: return False try : float (s) except ValueError: return False return True
解法二:正则表达式
依次来看下面的正则表达式:
匹配字符串开头^,可以有多个空格\s,且+-号只能出现一次
^\s*[+-]{0,1}
用于匹配诸如10.111、10.1、10等数字(小数点后面必须出现数字)
(\d)+((\.)(\d)+){0,1}
用于匹配.1、.111111等数字
((\.)(\d)+)
用于匹配10.、1.等数字(小数点后面没有数字)
((\d)+(\.))
e或E后面可以跟+-号,且后面必须跟数字。整个指数部分可以出现0-1次。
([eE][+-]{0,1}(\d)+){0,1}
整个字符串结束前可以跟0或多个空格
\s*$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import reclass Solution : def isNumber (self, s: str ) -> bool: matchObj = re.match("^\s*[+-]{0,1}((\d)+((\.)(\d)+){0,1}|((\.)(\d)+)|((\d)+(\.)))([eE][+-]{0,1}(\d)+){0,1}\s*$" ,s) if matchObj: print("match --> matchObj.group() : " , matchObj.group()) return True else : print("No match!!" ) return False so = Solution() print(so.isNumber("13.e2" ))
解法三:有限状态自动机
Stack valid-parentheses 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def isValid (self, s: str ) -> bool: stack = [] dic = {"{" : "}" , "[" : "]" , "(" : ")" } for c in s: if c in dic: stack.append(c) elif dic[stack.pop()] != c: return False return len (stack) == 0 so = Solution() print(so.isValid("()[]{}" ))
largest-rectangle-in-histogram 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 from typing import Listclass Solution : def largestRectangleArea (self, heights: List[int ] ) -> int: stack = [] res = 0 heights = [0 ] + heights + [0 ] for i in range (len (heights)): while stack and heights[i] < heights[stack[-1 ]]: tmp = stack.pop() res = max (res, (i - stack[-1 ] - 1 ) * heights[tmp]) stack.append(i) return res so = Solution() print(so.largestRectangleArea([2 , 1 , 5 , 6 , 2 , 3 ]))
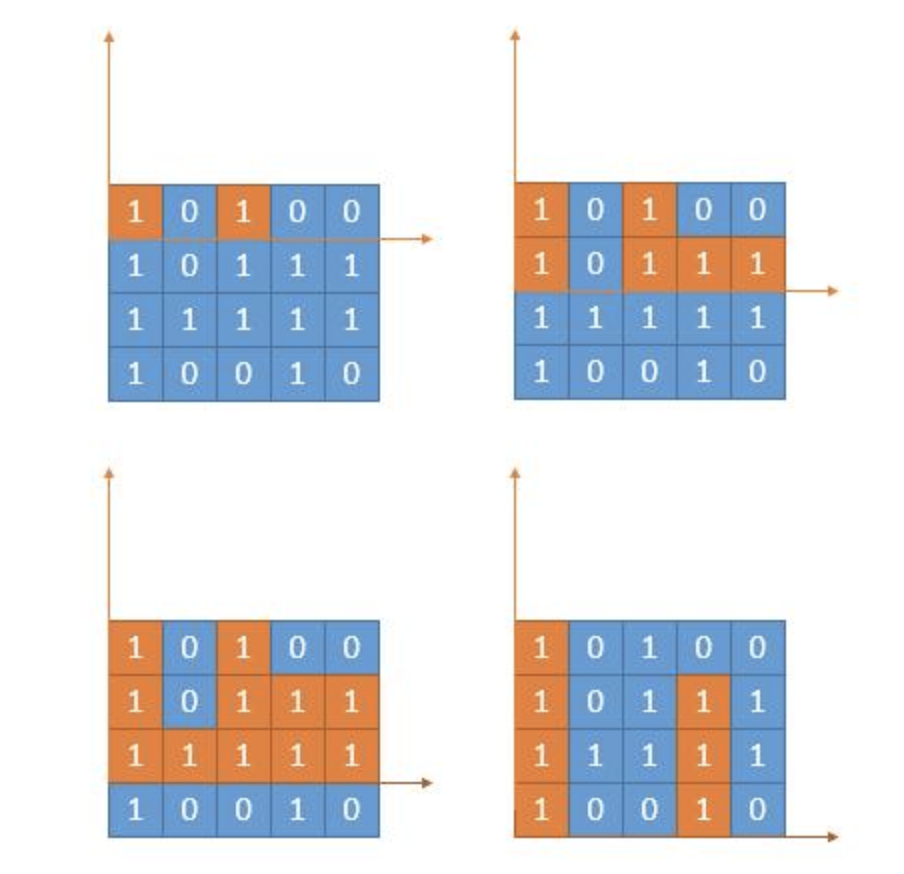
maximal-rectangle 注:参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 from typing import Listclass Solution : def maximalRectangle (self, matrix: List[List[str ]] ) -> int: max_area = 0 dp = [0 ] * len (matrix[0 ]) for row in range (0 , len (matrix)): for col in range (0 , len (matrix[0 ])): dp[col] = dp[col] + 1 if matrix[row][col] == "1" else 0 max_area = max (max_area, self.largestRectangleArea(dp)) return max_area def largestRectangleArea (self, heights: List[int ] ) -> int: stack = [] res = 0 heights = [0 ] + heights + [0 ] for i in range (len (heights)): while stack and heights[i] < heights[stack[-1 ]]: tmp = stack.pop() res = max (res, (i - stack[-1 ] - 1 ) * heights[tmp]) stack.append(i) return res so = Solution() print(so.maximalRectangle([ ["1" , "0" , "1" , "0" , "0" ], ["1" , "0" , "1" , "1" , "1" ], ["1" , "1" , "1" , "1" , "1" ], ["1" , "0" , "0" , "1" , "0" ] ]))
implement-queue-using-stacks 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 class MyQueue : def __init__ (self ): """ Initialize your data structure here. """ self.stack1 = [] self.stack2 = [] def push (self, x: int ) -> None : """ Push element x to the back of queue. """ self.stack1.append(x) def pop (self ) -> int: """ Removes the element from in front of queue and returns that element. """ if self.empty(): return if len (self.stack2) == 0 : while len (self.stack1) != 0 : self.stack2.append(self.stack1.pop()) return self.stack2.pop() def peek (self ) -> int: """ Get the front element. """ if self.empty(): return if len (self.stack2) == 0 : while len (self.stack1) != 0 : self.stack2.append(self.stack1.pop()) return self.stack2[-1 ] def empty (self ) -> bool: """ Returns whether the queue is empty. """ if len (self.stack1) == 0 and len (self.stack2) == 0 : return True return False
interview_20 解题思路:除了一个常规列表实现栈的操作外,再开一个辅助栈 用于保存当前的最小信息:
入栈操作:当辅助栈为空或者新元素小于等于辅助栈顶元素时,辅助栈入栈;否则无视
出栈操作:当常规栈中待出栈的元素等于辅助栈顶元素时,辅助栈出栈一个元素,代表当前的最小值出队或者次数减1
栈顶操作:仅需从常规栈顶取元素即可
最小值操作:因为辅助栈中维护的都是当前状态下的最小值,所以从辅助栈顶取元素即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class MinStack : def __init__ (self ): """ initialize your data structure here. """ self.stack = [] self.mins = [] def push (self, x: int ) -> None : self.stack.append(x) if not self.mins or x <= self.mins[-1 ]: self.mins.append(x) def pop (self ) -> None : if not self.stack: return x = self.stack.pop() if self.mins and self.mins[-1 ] == x: self.mins.pop() def top (self ) -> int: return self.stack and self.stack[-1 ] def min (self ) -> int: return self.mins and self.mins[-1 ]
interview_21 解题思路
我们使用一个辅助栈 来模拟该操作。将 pushed 数组中的每个数依次入栈,同时判断这个数是不是 popped 数组中下一个要 pop 的值,如果是就把它 pop 出来。最后检查栈是否为空。
算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 from typing import Listclass Solution : def validateStackSequences (self, pushed: List[int ], popped: List[int ] ) -> bool: i_pop = 0 stack = [] for value in pushed: stack.append(value) while stack and popped[i_pop] == stack[-1 ]: stack.pop() i_pop += 1 return not stack so = Solution() print(so.validateStackSequences(pushed=[1 , 2 , 3 , 4 , 5 ], popped=[4 , 5 , 3 , 2 , 1 ]))
interview_5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class MyQueue : def __init__ (self ): """ Initialize your data structure here. """ self.stack1 = [] self.stack2 = [] def push (self, x: int ) -> None : """ Push element x to the back of queue. """ self.stack1.append(x) def pop (self ) -> int: """ Removes the element from in front of queue and returns that element. """ if self.empty(): return if len (self.stack2) == 0 : while len (self.stack1) != 0 : self.stack2.append(self.stack1.pop()) return self.stack2.pop() def peek (self ) -> int: """ Get the front element. """ if self.empty(): return if len (self.stack2) == 0 : while len (self.stack1) != 0 : self.stack2.append(self.stack1.pop()) return self.stack2[-1 ] def empty (self ) -> bool: """ Returns whether the queue is empty. """ if len (self.stack1) == 0 and len (self.stack2) == 0 : return True return False
BinaryTree generate-parentheses 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def generateParenthesis (self, n: int ): output_li = [] def find_Parenthesis (s="" , left=0 , right=0 ): if len (s) == 2 * n: output_li.append(s) return if left < n: find_Parenthesis(s + "(" , left + 1 , right) if right < left: find_Parenthesis(s + ")" , left, right + 1 ) find_Parenthesis() return output_li so = Solution() print(so.generateParenthesis(2 ))
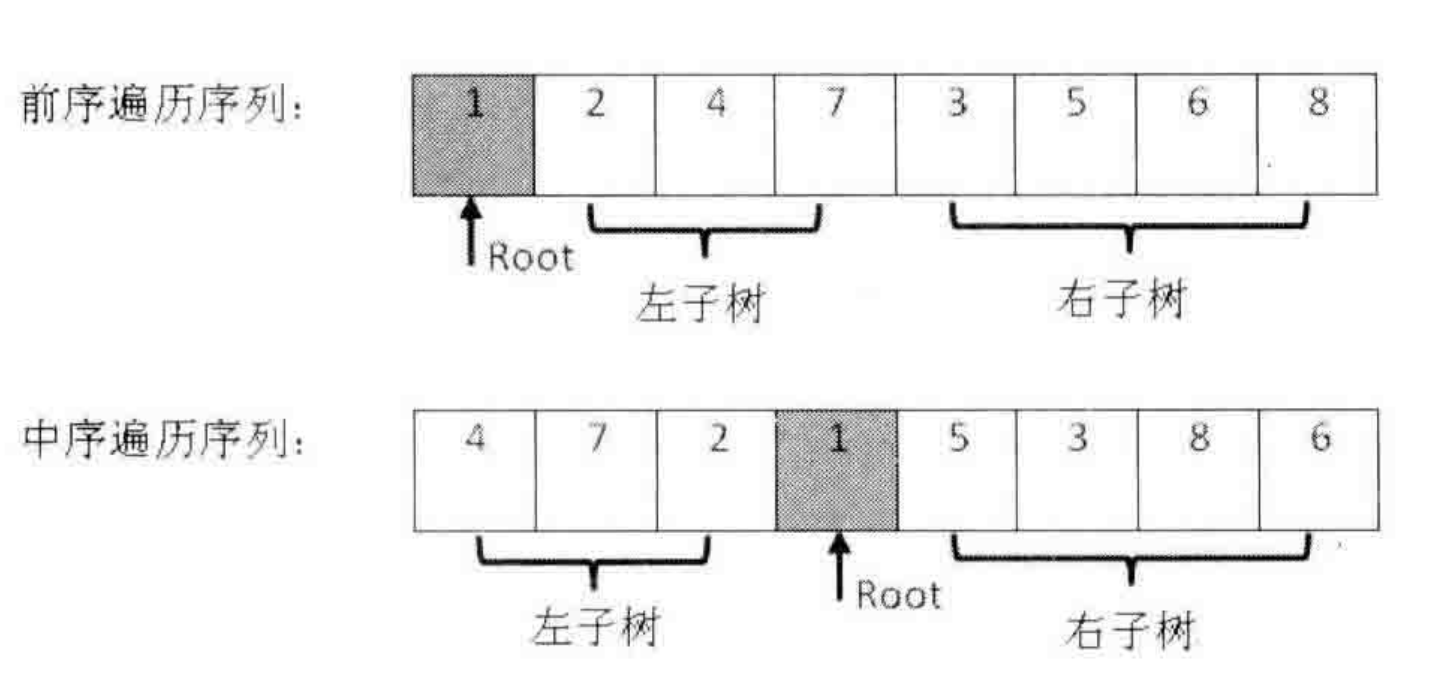
interview_4 解题思路:
前序遍历的第一个节点为根节点
根据前序遍历确定的根节点,可以在中序遍历中确定其左右子树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution (object def buildTree (self, preorder, inorder ): if not preorder: return None root_value = preorder[0 ] root = TreeNode(root_value) root_index = inorder.index(root_value) left_in_inorder = inorder[:root_index] right_in_inorder = inorder[root_index+1 :] left_in_preorder = preorder[1 :root_index+1 ] right_in_preorder = preorder[root_index+1 :] root.left = self.buildTree(left_in_preorder, left_in_inorder) root.right = self.buildTree(right_in_preorder, right_in_inorder) return root
interview_57 输入一个节点,分析该节点的下一个节点,一共有以下情况:
二叉树为空,则返回空;
该节点右孩子存在,则设置一个指针从该节点的右孩子出发,一直沿着指向左子结点的指针找到的叶子节点即为下一个节点;
该节点是其父节点的左孩子,则返回父节点;否则继续向上遍历其父节点的父节点,重复之前的判断,返回结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class TreeLinkNode : def __init__ (self, x ): self.val = x self.left = None self.right = None self.next = None class Solution : def GetNext (self, pNode ): if not pNode: return None if pNode.right: pNode = pNode.right while pNode.left: pNode = pNode.left return pNode while pNode.next : if pNode.next .left == pNode: return pNode.next pNode = pNode.next return None
longest-univalue-path 参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def longestUnivaluePath (self, root: TreeNode ) -> int: self.ans = 0 def arrow_length (node: TreeNode ): if node is None : return 0 left_length = arrow_length(node.left) right_length = arrow_length(node.right) left_arrow = right_arrow = 0 if node.left and node.val == node.left.val: left_arrow = left_length + 1 if node.right and node.val == node.right.val: right_arrow = right_length + 1 self.ans = max (self.ans, left_arrow+right_arrow) return max (left_arrow, right_arrow) arrow_length(root) return self.ans
interview_17 解题思路
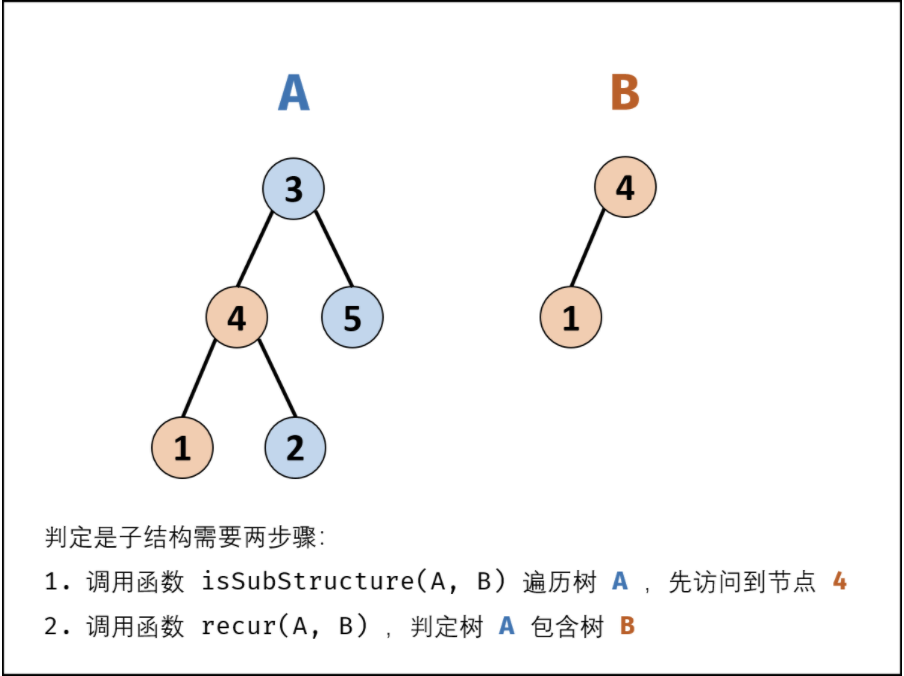
若树 B 是树 A 的子结构,则子结构的根节点可能为树 A 的任意一个节点。因此,判断树 B 是否是树 A 的子结构,需完成以下两步工作:
先序遍历树 A中的每个节点 A。(对应函数 isSubStructure(A, B))
判断树 A 中 以A为根节点的子树 是否包含树 B 。(对应函数 recur(A, B))
特例处理: 当 树 A 为空 或 树 B 为空 时,直接返回 false ;
终止条件:
返回值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def isSubStructure (self, A: TreeNode, B: TreeNode ) -> bool: if not A or not B: return False return self.recure(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B) def recure (self, A: TreeNode, B: TreeNode ) -> bool: if not B: return True if not A or A.val != B.val: return False return self.recure(A.left, B.left) and self.recure(A.right, B.right)
invert-binary-tree
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def invertTree (self, root: TreeNode ) -> TreeNode: if not root: return root left = self.invertTree(root.left) right = self.invertTree(root.right) root.left = right root.right = left return root
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def invertTree (self, root: TreeNode ) -> TreeNode: if not root: return root queue = [root] while queue: temp_root = queue.pop() temp_root.left, temp_root.right = temp_root.right, temp_root.left if temp_root.left: queue.append(temp_root.left) if temp_root.right: queue.append(temp_root.right) return root
interview_22_i 利用队列,广度优先遍历二叉树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from typing import Listimport collectionsclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def levelOrder (self, root: TreeNode ) -> List[int]: if not root: return [] res, deque = [], collections.deque() deque.append(root) while deque: node = deque.popleft() res.append(node.val) if node.left: deque.append(node.left) if node.right: deque.append(node.right) return res
interview_22_ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 from typing import Listimport collectionsclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def levelOrder (self, root: TreeNode ) -> List[List[int]]: if not root: return [] res, deque = [], collections.deque() deque.append(root) while deque: tem = [] for _ in range (len (deque)): node = deque.popleft() tem.append(node.val) if node.left: deque.append(node.left) if node.right: deque.append(node.right) res.append(tem) return res
interview_22_iii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 from typing import Listimport collectionsclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def levelOrder (self, root: TreeNode ) -> List[List[int]]: if not root: return [] res, deque = [], collections.deque() deque.append(root) while deque: tem = [] for _ in range (len (deque)): node = deque.popleft() tem.append(node.val) if node.left: deque.append(node.left) if node.right: deque.append(node.right) res.append(tem[::-1 ] if len (res) % 2 else tem) return res
interview_59 此题同interview_22_iii
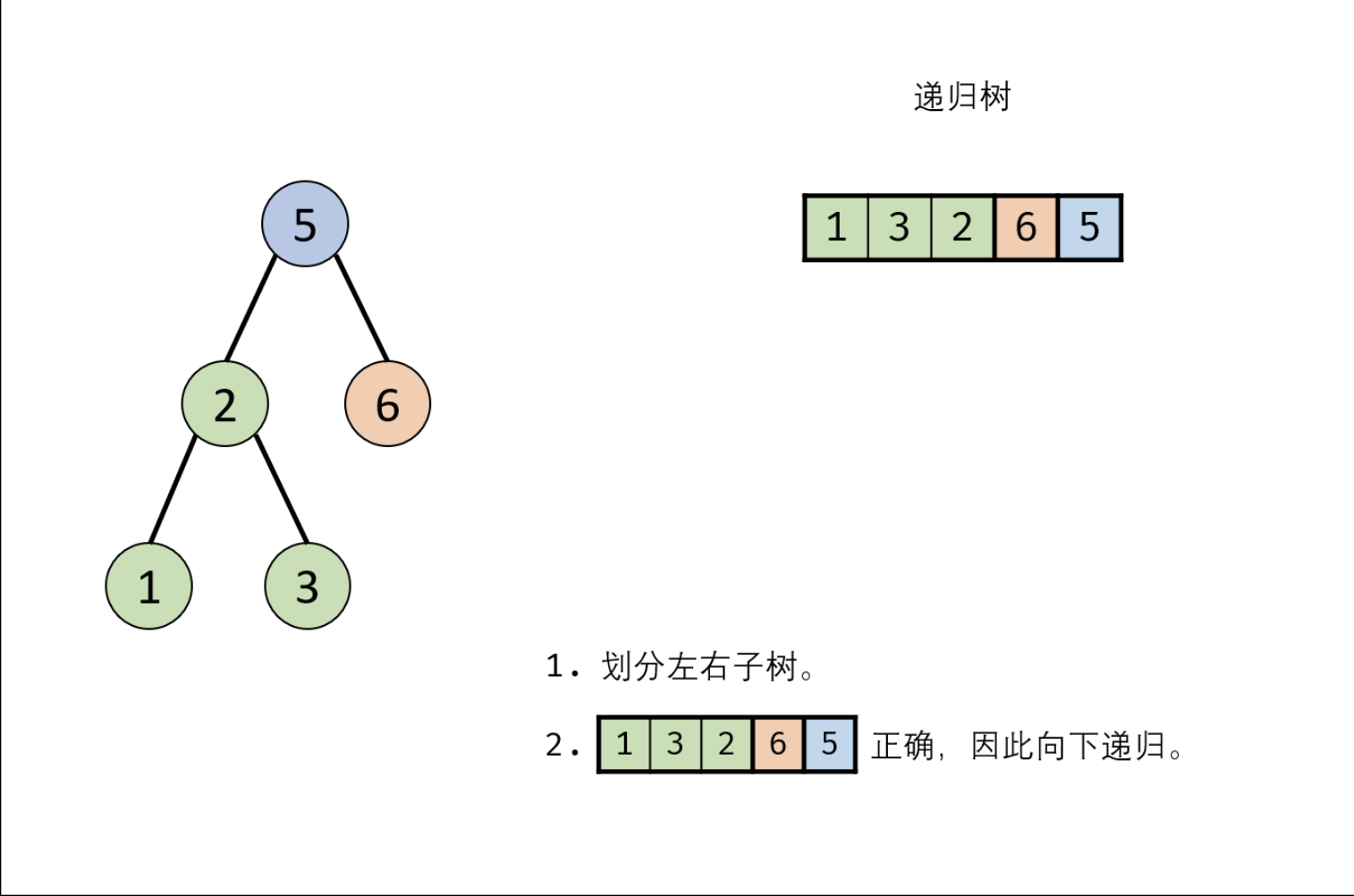
interview_23 解题思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 from typing import Listclass Solution : def verifyPostorder (self, postorder: List[int ] ) -> bool: if not postorder: return False def recur (i, j ): if i >= j: return True p = i while postorder[p] < postorder[j]: p += 1 left_end = p while postorder[p] > postorder[j]: p += 1 return p == j and recur(i, left_end - 1 ) and recur(left_end, j - 1 ) return recur(0 , len (postorder) - 1 ) so = Solution() print(so.verifyPostorder([1 , 3 , 2 , 6 , 5 ]))
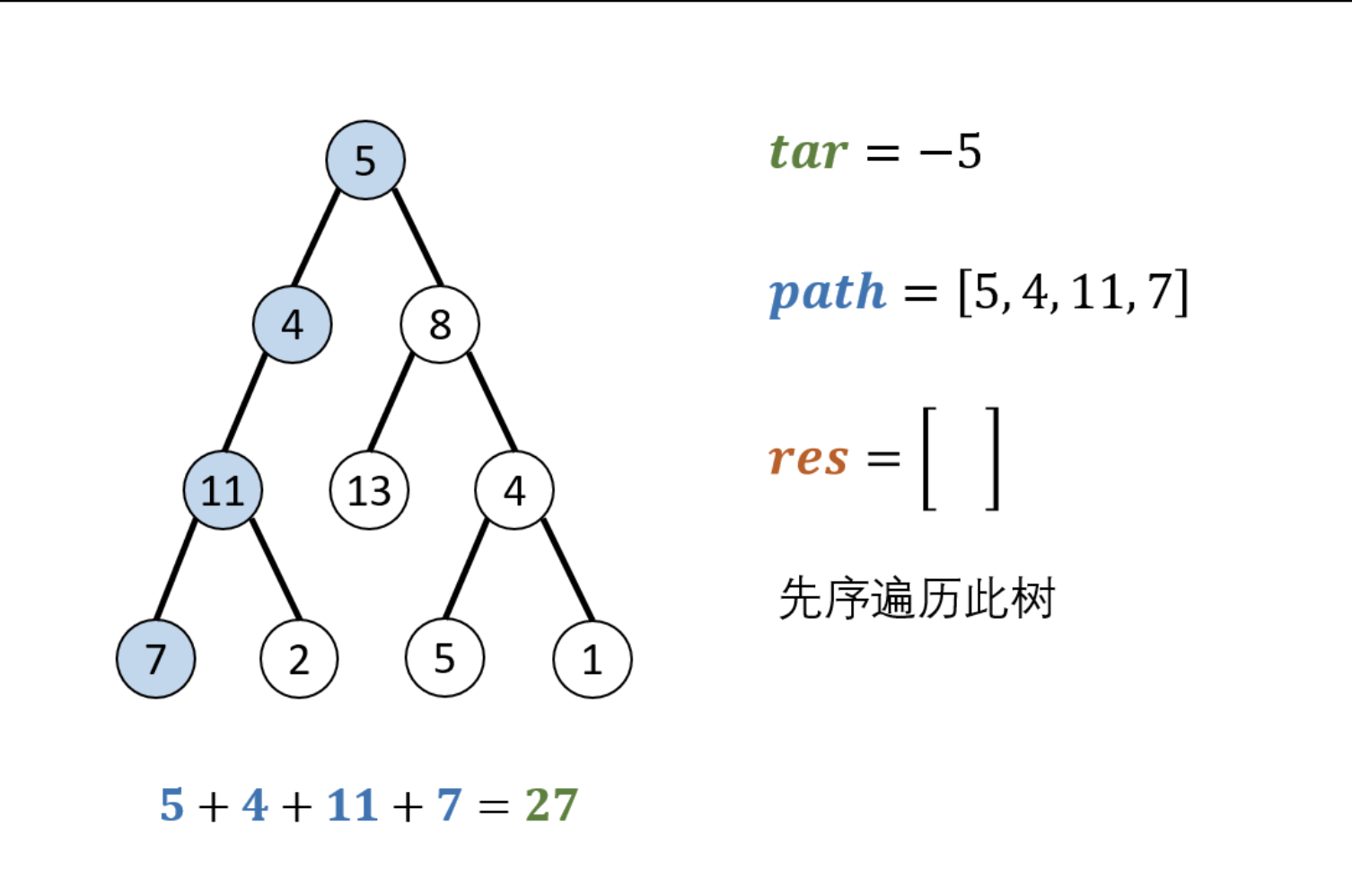
interview_24 本问题是典型的二叉树方案搜索问题,使用回溯法解决 ,其包含 先序遍历 + 路径记录 两部分。
参考链接
res.append(list(path)):记录路径时若直接执行 res.append(path) ,则是将 path 列表对象 加入了 res ;后续 path 对象改变时, res 中的 path 对象 也会随之改变(因此肯定是不对的,本来存的是正确的路径 path ,后面又 append 又 pop 的,就破坏了这个正确路径)。list(path) 相当于新建并复制了一个 path 列表,因此不会受到 path 变化的影响。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from typing import Listclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def pathSum (self, root: TreeNode, sum : int ) -> List[List[int]]: res, path = [], [] def recur (root, tar ): if not root: return path.append(root.val) tar -= root.val if tar == 0 and not root.left and not root.right: res.append(list (path)) recur(root.left, tar) recur(root.right, tar) path.pop() recur(root, sum ) return res
interview_26 参考链接
算法流程:dfs(cur): 递归法中序遍历;
终止条件 : 当节点 cur为空,代表越过叶节点,直接返回;
递归左子树,即 dfs(cur.left);
构建链表 :
当 pre 为空时 : 代表正在访问链表头节点,记为 head 。当 pre 不为空时 : 修改双向节点引用,即 pre.right = cur ,cur.left = pre;
保存 cur : 更新 pre = cur ,即节点 cur 是后继节点的 pre;
递归右子树,即 dfs(cur.right) ;
treeToDoublyList(root):
特例处理 : 若节点 root为空,则直接返回;初始化 : 空节点 pre;转化为双向链表 : 调用 dfs(root) ;构建循环链表 : 中序遍历完成后,head指向头节点, pre指向尾节点,因此修改 head 和 pre的双向节点引用即可。返回值 : 返回链表的头节点 head 即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 """ # Definition for a Node. class Node: def __init__(self, val, left=None, right=None): self.val = val self.left = left self.right = right """ class Solution : def __init (self ): self.pre = None self.head = None def Convert (self, pRootOfTree ): def dfs (current_node ): if not current_node: return dfs(current_node.left) if not self.pre: self.head = current_node else : self.pre.right, current_node.left = current_node, self.pre self.pre = current_node dfs(current_node.right) if not pRootOfTree: return dfs(pRootOfTree) self.pre.right, self.head.left = self.head, self.pre return self.head
interview_18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def mirrorTree (self, root: TreeNode ) -> TreeNode: if not root: return None root.left, root.right = root.right, root.left self.mirrorTree(root.left) self.mirrorTree(root.right) return root def mirrorTree_diedai (self, root: TreeNode ) -> TreeNode: if not root: return None queue = [root] while queue: node = queue.pop(0 ) node.left, node.right = node.right, node.left if node.left: queue.append(node.left) if node.right: queue.append(node.right) return root
interview_22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 from typing import Listimport collectionsclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def levelOrder (self, root: TreeNode ) -> List[int]: if not root: return [] res, deque = [], collections.deque() deque.append(root) while deque: node = deque.popleft() res.append(node.val) if node.left: deque.append(node.left) if node.right: deque.append(node.right) return res
maximum-depth-of-binary-tree interview_38 此题同maximum-depth-of-binary-tree
深度优先遍历DFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def maxDepth (self, root: TreeNode ) -> int: if not root: return 0 return max (self.maxDepth(root.left), self.maxDepth(root.right)) + 1
广度优先遍历BFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def maxDepth (self, root: TreeNode ) -> int: if not root: return 0 queue = [root] result = 0 while queue: tmp = [] for node in queue: if node.left: tmp.append(node.left) if node.right: tmp.append(node.right) queue = tmp result += 1 return result
interview_39 思路参考
思路是构造一个获取当前子树的深度的函数 depth(root) ,通过比较某子树的左右子树的深度差 abs(depth(root.left) - depth(root.right)) <= 1 是否成立,来判断某子树是否是二叉平衡树。若所有子树都平衡,则此树平衡。
算法流程:
特例处理: 若树根节点 root 为空,则直接返回 true ;
abs(self.depth(root.left) - self.depth(root.right)) <= 1 :判断 当前子树 是否是平衡树;
self.isBalanced(root.left) : 先序遍历递归,判断 当前子树的左子树 是否是平衡树;
self.isBalanced(root.right) : 先序遍历递归,判断 当前子树的右子树 是否是平衡树;
depth(root) 函数: 计算树 root 的深度
终止条件: 当 root 为空,即越过叶子节点,则返回高度 0 ;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution : def isBalanced (self, root: TreeNode ) -> bool: if not root: return True return abs (self.depth(root.left) - self.depth(root.right)) <= 1 \ and self.isBalanced(root.left) \ and self.isBalanced(root.right) def depth (self, root ): if not root: return 0 return max (self.depth(root.left), self.depth(root.right)) + 1
interview_58 解题思路参考
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def isSymmetric (self, root: TreeNode ) -> bool: def recur (LeftNode, RightNode ): if not LeftNode and not RightNode: return True if not LeftNode or not RightNode or LeftNode.val != RightNode.val: return False return recur(LeftNode.left, RightNode.right) and recur(LeftNode.right, RightNode.left) return recur(root.left, root.right) if root else True
interview_61 参考链接
序列化操作:类似于BFS,不同之处则是需要增加空结点的处理。
反序列化操作:由于序列化时建立了一颗“满二叉树”,则可基于叶结点和父结点之间的关系 ,对已序列化的结果进行反序列化。关系见下:
如果从下标bai从1开始存储,则编号为i的结点的主要关系为:
如果从下标从0开始存储,则编号为i的结点的主要关系为:
反序列化算法逻辑为:
特例处理: 若 data为空,直接返回 null;
初始化: 序列化列表 vals(先去掉首尾中括号,再用逗号隔开),指针 i = 1 ,根节点 root(值为 vals[0] ),队列 queue(包含 root);
按层构建: 当 queue 为空时跳出;
节点出队,记为 node;
构建 node的左子节点:node.left 的值为 vals[i],并将 node.left入队;
执行 i+=1;
构建 node的右子节点:node.left的值为 vals[i],并将 node.left入队;
执行 i+=1;
返回值: 返回根节点root即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 from collections import dequeclass TreeNode (object def __init__ (self, x ): self.val = x self.left = None self.right = None class Codec : def serialize (self, root ): """Encodes a tree to a single string. :type root: TreeNode :rtype: str """ if not root: return "[]" result, de = [], deque() de.append(root) while de: node = de.popleft() if node: result.append(str (node.val)) de.append(node.left) de.append(node.right) else : result.append("null" ) return "[" +"," .join(result)+"]" def deserialize (self, data ): """Decodes your encoded data to tree. :type data: str :rtype: TreeNode """ if data == "[]" : return values, i = data[1 :-1 ].split("," ), 1 root = TreeNode(values[0 ]) de = deque() de.append(root) while de: node = de.popleft() if values[i] != "null" : node.left = TreeNode(int (values[i])) de.append(node.left) i += 1 if values[i] != "null" : node.right = TreeNode(int (values[i])) de.append(node.right) i += 1 return root
interview_62 参考链接
二叉搜索树的中序遍历为递增序列 。因此求二叉搜索树的第K大的结点为为求此二叉搜索树中序遍历倒序的第K大的结点。 (即中序遍历是会产生一个从小到大的排列[1, 2, 3, 4, 5],中序遍历的倒序则是产生一个从大到小的排列[5, 4, 3, 2, 1])
中序遍历递归顺序为:
1 2 3 4 5 6 def dfs (root ): if not root: return dfs(root.left) print(root.val) dfs(root.right)
倒序为
1 2 3 4 5 6 def dfs (root ): if not root: return dfs(root.right) print(root.val) dfs(root.left)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def __init__ (self ): self.k = None self.result_node = None def kthLargest (self, root: TreeNode, k: int ) -> int: def dfs (root ): if not root or self.k == 0 : return dfs(root.right) self.k -= 1 if self.k == 0 : self.result_node = root.val dfs(root.left) self.k = k dfs(root) return self.result_node
Tree
binary-tree-inorder-traversal 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 from typing import Listclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def inorderTraversal (self, root: TreeNode ) -> List[int]: res = [] def backtrack (root ): if not root: return backtrack(root.left) res.append(root.val) backtrack(root.right) backtrack(root) return res root = TreeNode(1 ) root.left = TreeNode(2 ) root.right = TreeNode(3 ) so = Solution() print(so.inorderTraversal(root))
unique-binary-search-trees-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from typing import Listclass TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def generateTrees (self, n: int ) -> List[TreeNode]: def generate_tree (start, end ): if start > end: return [None , ] all_trees = [] for i in range (start, end+1 ): left_tree = generate_tree(start, i) right_tree = generate_tree(i+1 , end) for left in left_tree: for right in right_tree: current_tree = TreeNode(i) current_tree.left = TreeNode(left) current_tree.right = TreeNode(right) all_trees.append(current_tree) return all_trees return generate_tree(1 , n) if n else []
unique-binary-search-trees 假设n个节点存在
令G(n)的从1到n可以形成二叉排序树个数
令f(i)为以i为根的二叉搜索树的个数
即有: G(n) = f(1) + f(2) + f(3) + f(4) + ... + f(n)
n为根节点,当i为根节点时,其左子树节点个数为[1,2,3,...,i-1],右子树节点个数为[i+1,i+2,...n],所以当i为根节点时,其左子树节点个数为i-1个,右子树节点为n-i,即f(i) = G(i-1)*G(n-i)
上面两式可得:G(n) = G(0)*G(n-1) + G(1)*(n-2) +...+ G(n-1)*G(0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def numTrees (self, n: int ) -> int: if n < 0 : return 0 dp = [0 for _ in range (n+1 )] dp[0 ] = 1 dp[1 ] = 1 for i in range (2 , n+1 ): for j in range (i): dp[i] += dp[j] * dp[i - j - 1 ] return dp[-1 ] so = Solution() print(so.numTrees(3 ))
validate-binary-search-tree 需要在遍历树的同时保留结点的上界与下界,在比较时不仅比较子结点的值,也要与上下界比较。这样才能保证节点的所有左子树都小于结点值,右子树都大于结点值。
参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def isValidBST (self, root: TreeNode ) -> bool: if not root: return True stack = [(root, float ('-inf' ), float ('inf' )), ] while stack: root, lower, upper = stack.pop() if not root: continue val = root.val if val <= lower or val >= upper: return False stack.append((root.right, val, upper)) stack.append((root.left, lower, val)) return True
recover-binary-search-tree 参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def __init__ (self ): self.pre_node = TreeNode(float ("-inf" )) self.second_node = None self.first_node = None def recoverTree (self, root: TreeNode ) -> None : """ Do not return anything, modify root in-place instead. """ def in_order (root ): if not root: return in_order(root.left) if self.first_node is None and self.pre_node.val >= root.val: self.first_node = self.pre_node if self.first_node is not None and self.pre_node.val >= root.val: self.second_node = root self.pre_node = root in_order(root.right) in_order(root) self.first_node.val, self.second_node.val = self.second_node.val, self.first_node.val
same-tree 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class TreeNode : def __init__ (self, x ): self.val = x self.left = None self.right = None class Solution : def isSameTree (self, p: TreeNode, q: TreeNode ) -> bool: if not p and not q: return True if not p or not q: return False if p.val != q.val: return True return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
Queue merge-k-sorted-lists 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from queue import PriorityQueueclass ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def mergeKLists (self, lists ) -> ListNode: head_pre = p = ListNode(0 ) prior_queue = PriorityQueue() for list_node in lists: if list_node: prior_queue.put((list_node.val, list_node)) while not prior_queue.empty(): node_val, node = prior_queue.get() p.next = ListNode(node_val) p = p.next node = node.next if node: prior_queue.put((node.val, node)) return head_pre.next
Bit Operation divide-two-integers 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution : def divide (self, dividend: int , divisor: int ) -> int: flag = dividend < 0 ^ divisor < 0 dividend, divisor = abs (dividend), abs (divisor) result = 0 move_step = 0 while divisor <= dividend: move_step += 1 divisor <<= 1 while move_step > 0 : move_step -= 1 divisor >>= 1 if dividend >= divisor: result += 1 << move_step dividend -= divisor if not flag: result = -result return result if -(1 << 31 ) <= result <= (1 << 31 ) - 1 else (1 << 31 ) - 1 so = Solution() print(so.divide(-45 , 2 ))
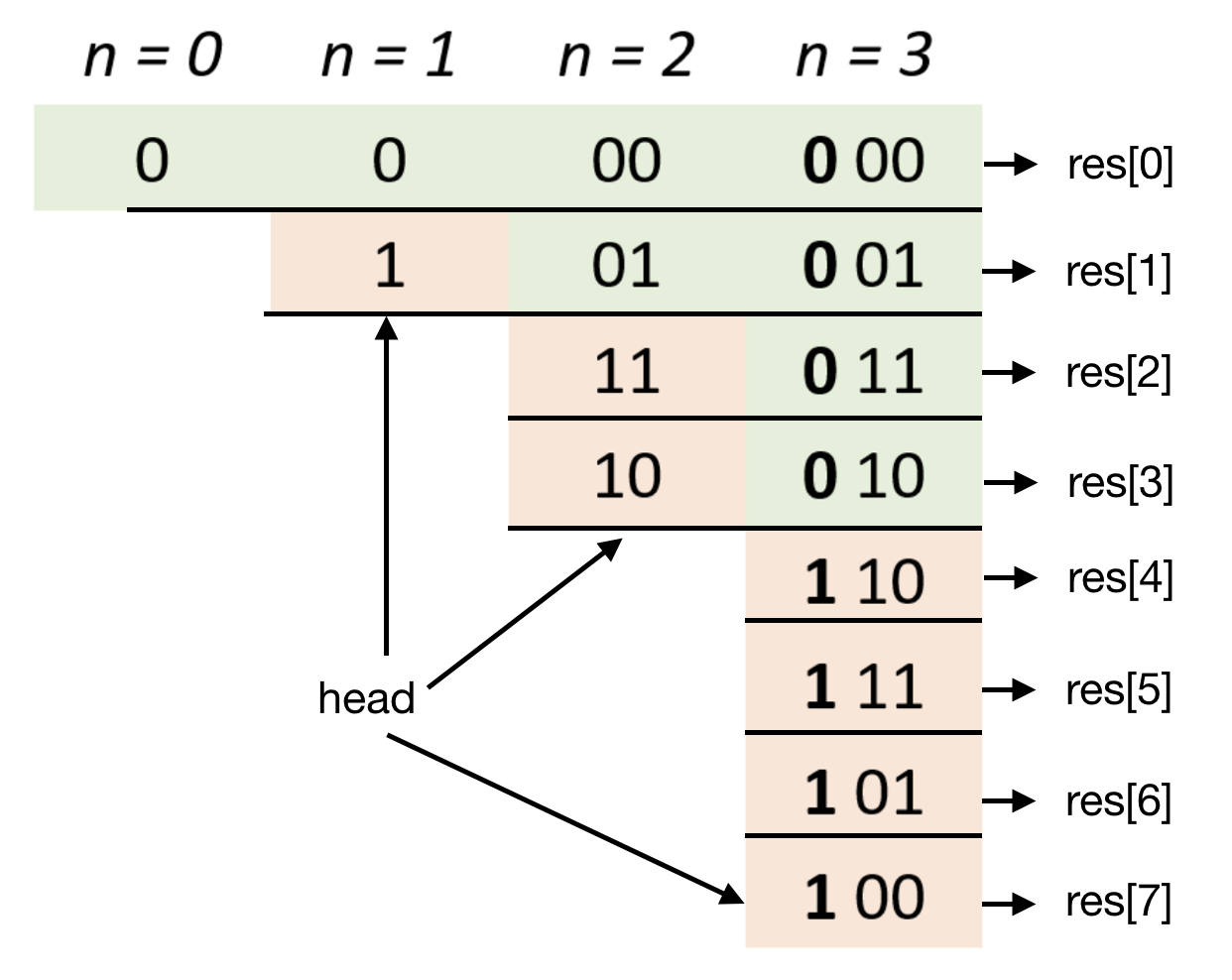
gray-code 解题思路:
结果是当前head的移位结果 + 已有结果的倒序(注:参考链接 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 from typing import Listclass Solution : def grayCode (self, n: int ) -> List[int]: res, head = [0 ], 1 for i in range (n): for j in range (len (res) - 1 , -1 , -1 ): res.append(head + res[j]) head <<= 1 return res so = Solution() print(so.grayCode(2 ))
convert-a-number-to-hexadecimal 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def toHex (self, num: int ) -> str: num &= 0xFFFFFFFF mask = 0b1111 s = "0123456789abcdef" result = "" while num > 0 : result += s[num & mask] num >>= 4 return result[::-1 ] if result else "0" so = Solution() print(so.toHex(26 ))
binary-watch 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def readBinaryWatch (self, num: int ) -> List[str]: def count_binary_1 (i ): return bin (i).count("1" ) dict_binary = {i: count_binary_1(i) for i in range (60 )} res = [] for h in range (12 ): for m in range (60 ): if dict_binary[h] + dict_binary[m] == num: hour = str (h) m = str (m) if m > 9 else "0" + str (m) res.append(hour + ":" + m) return res so = Solution() print(so.readBinaryWatch(1 ))
interview_11 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def hammingWeight (self, n: int ) -> int: res = 0 count = 1 while n and count <= 32 : res += n & 1 n >>= 1 count += 1 return res so = Solution() print(so.hammingWeight(-1 ))
interview_48 题解来源
因为不允许采用四则运算,所以只能考虑位运算了。
其实就是用二进制来模拟加法操作。首先将两个数最低位相加,如果都是 1 ,那么就得到 0 ,并且进位 1 ,然后接着算下一位。
但是这样一位一位模拟不方便实现,更简单的实现方法是直接把两个数对应位相加,不管进位。然后进位单独计算,如果某一位两个数都是 1 ,那么进位就会对下一位产生影响。然后接着算不进位求和加上进位的值,再计算新的进位,依次重复下去,直到进位为 0 为止。
用一个实际的例子来演示一下,计算 3+7 的值,其中 s 表示每一步不考虑进位的求和,c 表示每一步的进位,最后得到结果 1010 ,也就是十进制的 10
Python 负数的存储:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def add (self, a: int , b: int ) -> int: a &= 0xffffffff b &= 0xffffffff while b != 0 : c = ((a & b) << 1 ) & 0xffffffff a ^= b b = c return a if a <= 0x7fffffff else ~(a ^ 0xffffffff ) so = Solution() print(so.add(-3 , -2 ))
interview_49 参考链接
数字越界处理:
题目要求返回的数值范围应在[ -2^31, 2 ^ 31 − 1] ,因此需要考虑数字越界问题。而由于题目指出环境只能存储 32 位大小的有符号整数 ,因此判断数字越界时,要始终保持 res 在 int 类型的取值范围内。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution : def strToInt (self, str : str ) -> int: if not str : return 0 result, i, sign, len_str = 0 , 0 , 1 , len (str ) int_max, int_min, boundary = 2 ** 31 - 1 , -2 ** 31 , 2 ** 31 // 10 while str [i] == " " : i += 1 if i == len_str: return 0 if str [i] == "-" : sign = -1 if str [i] in ("+" , "-" ): i += 1 for c in str [i:]: if not "0" <= c <= "9" : break if result > boundary or (result == boundary and c > "7" ): return int_max if sign == 1 else int_min result = result * 10 + ord (c) - ord ("0" ) return sign * result so = Solution() print(so.strToInt("+123i adf" ))
支持小数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution : def strToInt (self, str : str ) -> int: if not str : return 0 result, i, sign, len_str = 0 , 0 , 1 , len (str ) int_max, int_min, boundary = 2 ** 31 - 1 , -(2 ** 31 ), 2 ** 31 // 10 while str [i] == " " : i += 1 if i == len_str: return 0 if str [i] == "-" : sign = -1 if str [i] in ("+" , "-" ): i += 1 for c in str [i:]: i += 1 if not "0" <= c <= "9" : break if result > boundary or (result == boundary and c > "7" ): return int_max if sign == 1 else int_min result = result * 10 + ord (c) - ord ("0" ) x = 1 if str [i-1 ] == "." : for c in str [i:]: if not "0" <= c <= "9" : break if result > boundary or (result == boundary and c > "7" ): return int_max if sign == 1 else int_min result = result + (ord (c) - ord ("0" )) * 0.1 ** x x += 1 return sign * result so = Solution() print(so.strToInt("+12.3" ))
Binary Search find-first-and-last-position-of-element-in-sorted-array 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def find_left_right_index (self, nums, target, left_right_flag ): left, right = 0 , len (nums) while left < right: mid = (left + right) // 2 if nums[mid] > target or (left_right_flag and nums[mid] == target): right = mid else : left = mid + 1 return left def searchRange (self, nums, target: int ): left_index = self.find_left_right_index(nums, target, True ) if left_index == len (nums) or nums[left_index] != target: return [-1 , -1 ] return [left_index, self.find_left_right_index(nums, target, False ) - 1 ] so = Solution() print(so.searchRange([5 , 7 , 7 , 8 , 8 , 10 ], 8 ))
sqrtx 当x ≥ 2 时,它的整数平方根一定小于 x / 2。由于结果一定是整数,此问题可以转换成在有序整数集中寻找一个特定值,因此可以使用二分查找。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def mySqrt (self, x: int ) -> int: if x < 2 : return x left = 2 right = x // 2 while left <= right: middle = left + (right - left) // 2 if middle * middle > x: right = middle - 1 elif middle * middle < x: left = middle + 1 else : return middle return right so = Solution() print(so.mySqrt(8 ))
search-a-2d-matrix 将整个matric当做一个列表,进行二分查找。其中对应的元素与其行列的索引为:
middle = (left + right) // 2
row_index = middle // cols
col_index = middle % cols
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from typing import Listclass Solution : def searchMatrix (self, matrix: List[List[int ]], target: int ) -> bool: if not matrix or len (matrix) == 0 : return False rows = len (matrix) cols = len (matrix[0 ]) left = 0 right = rows * cols - 1 while left <= right: middle = (left + right) // 2 row = middle // cols col = middle % cols if matrix[row][col] == target: return True if matrix[row][col] > target: right = middle - 1 else : left = middle + 1 return False so = Solution() print(so.searchMatrix([ [1 , 3 , 5 , 7 ], [10 , 11 , 16 , 20 ], [23 , 30 , 34 , 50 ] ], 3 ))
search-in-rotated-sorted-array 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution : def search (self, nums, target: int ) -> int: if not nums: return -1 left, right = 0 , len (nums) - 1 while left <= right: mid = (left + right) // 2 if nums[mid] == target: return mid if nums[mid] < nums[right]: if nums[mid] < target < nums[right]: left = mid + 1 else : right = mid - 1 else : if nums[left] < target < nums[mid]: right = mid - 1 else : left = mid + 1 return -1 so = Solution() print(so.search([4 , 5 , 6 , 7 , 0 , 1 , 2 ], 0 ))
find-minimum-in-rotated-sorted-array 参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 from typing import Listclass Solution : def findMin (self, nums: List[int ] ) -> int: len_nums = len (nums) if len_nums <= 1 : return nums[0 ] left = 0 right = len_nums - 1 while left <= right: middle = (left + right) // 2 if nums[middle - 1 ] > nums[middle]: return nums[middle] if nums[middle] > nums[middle + 1 ]: return nums[middle + 1 ] if nums[middle] > nums[left]: left = middle + 1 else : right = middle - 1 so = Solution() print(so.findMin([3 , 4 , 5 , 1 , 2 ]))
search-in-rotated-sorted-array-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution : def search (self, nums, target: int ) -> int: if not nums: return False left, right = 0 , len (nums) - 1 while left <= right: mid = (left + right) // 2 if nums[mid] == target: return True if nums[mid] < nums[right]: if nums[mid] < target < nums[right]: left = mid + 1 else : right = mid - 1 else : if nums[left] < target < nums[mid]: right = mid - 1 else : left = mid + 1 return False so = Solution() print(so.search([2 , 5 , 6 , 0 , 0 , 1 , 2 ], 3 ))
min-value-in-rotated-array 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def minNumberInRotateArray (self, rotateArray ): len_rotatearray = len (rotateArray) if len_rotatearray <= 1 : return rotateArray left = 0 right = len_rotatearray - 1 while left < right: middle = (left + right) // 2 if rotateArray[middle] > rotateArray[right]: left = middle + 1 else : right = middle return rotateArray[left] so = Solution() print(so.minNumberInRotateArray([1 , 2 , 3 , 4 , 5 , 6 , 7 ])) print(so.minNumberInRotateArray([4 , 5 , 6 , 7 , 1 , 2 , 3 ])) print(so.minNumberInRotateArray([6 , 7 , 1 , 2 , 3 , 4 , 5 ]))
find-peak-element
时间复杂度 : O(log_2(n))。 每一步都将搜索空间减半。因此,总的搜索空间只需要 log_2(n)步。其中 n 为 num 数组的长度。
空间复杂度 : O(1)。 只使用了常数空间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 from typing import Listclass Solution : def findPeakElement (self, nums: List[int ] ) -> int: left = 0 right = len (nums) - 1 while left < right: middle = (left + right) // 2 if nums[middle] > nums[middle + 1 ]: right = middle else : left = middle + 1 return left so = Solution() print(so.findPeakElement([1 , 2 , 1 , 3 , 5 , 6 , 4 ]))
interview_50 参考链接
时间复杂度O(N)
空间复杂度O(N)
1 2 3 4 5 6 7 class Solution : def findRepeatNumber (self, nums: [int ] ) -> int: dic = set () for num in nums: if num in dic: return num dic.add(num) return -1
时间复杂度O(N)
空间复杂度O(1)
索引处存放的值为对应的索引。
注:此方法不能保证重复数字出现的先后顺序(若有两个重复数字,如果需要返回第一个重复的数字,那么此方法不能保证返回的顺序正确)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def findRepeatNumber (self, nums: List[int ] ) -> int: if not nums: return -1 i = 0 while i < len (nums): if nums[i] == i: i += 1 continue if nums[i] == nums[nums[i]]: return nums[i] nums[nums[i]], nums[i] = nums[i], nums[nums[i]] return -1
interview_6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def minNumberInRotateArray (self, rotateArray ): len_rotatearray = len (rotateArray) if len_rotatearray <= 1 : return rotateArray left = 0 right = len_rotatearray - 1 while left < right: middle = (left + right) // 2 if rotateArray[middle] > rotateArray[right]: left = middle + 1 else : right = middle return rotateArray[left] so = Solution() print(so.minNumberInRotateArray([1 , 2 , 3 , 4 , 5 , 6 , 7 ])) print(so.minNumberInRotateArray([4 , 5 , 6 , 7 , 1 , 2 , 3 ])) print(so.minNumberInRotateArray([6 , 7 , 1 , 2 , 3 , 4 , 5 ]))
interview_37 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def GetNumberOfK (self, data, k ): if not data: return 0 len_data = len (data) left, right = 0 , 0 for i in range (0 , len_data - 1 ): if data[i] == k: left = i break for j in range (len_data - 1 , -1 , -1 ): if data[j] == k: right = j break if left == 0 and right == 0 : if data[left] == k: return 1 else : return 0 return right - left + 1
Double Pointer trapping-rain-water 直接思路:
对于每个元素而言,它对应的水的数量由其左右两边最大的高度决定,即:
当前元素向左扫描得到最大的高度max_left_height
当前元素向右扫描得到最大的高度max_right_height
取min(max_left_height, max_right_height),得到min_height
再将min_height 与当前元素的height相减,即为当前元素所能注得的水量
时间复杂度: $O(n^2)$ ,因数组中的每个元素都需要向左向右扫描。
本题采用双指针法:时间复杂度为 $O(n)$ ,空间复杂度为 $O(1)$
思路如下:
伪代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from typing import Listclass Solution : def trap (self, height: List[int ] ) -> int: if not height: return 0 left, right = 0 , len (height) - 1 left_max, right_max = height[left], height[right] result = 0 while left < right: if height[left] < height[right]: if height[left] >= left_max: left_max = height[left] else : result += (left_max - height[left]) left += 1 else : if height[right] >= right_max: right_max = height[right] else : result += (right_max - height[right]) right -= 1 return result so = Solution() print(so.trap([0 , 1 , 0 , 2 , 1 , 0 , 1 , 3 , 2 , 1 , 2 , 1 ]))
sort-colors 解题思路:
left指向0、right指向2
当nums[current] = 0或2时,跟left、right指向的元素进行交换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 from typing import Listclass Solution : def sortColors (self, nums: List[int ] ) -> List: if len (nums) <= 1 : return nums left = 0 right = len (nums) - 1 current = 0 while left <= right: if nums[current] == 0 : nums[left], nums[current] = nums[current], nums[left] left += 1 current += 1 elif nums[current] == 1 : nums[right], nums[current] = nums[current], nums[right] right -= 1 else : current += 1 return nums so = Solution() print(so.sortColors([2 , 0 , 2 , 1 , 1 , 0 ]))
minimum-window-substring 解题思路:
滑动窗口的思想
left指针仅在当前窗口满足条件之后才会移动:即当前窗口中满足要求,left会试着移动以此减少结果的长度
right 指针不停向右移动,找寻满足条件的窗口
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 from collections import Counterfrom collections import defaultdictclass Solution1 : def minWindow1 (self, s: str , t: str ) -> str: left, right = 0 , 0 length_s = len (s) result = s + s t_dict = Counter(t) count_dict = defaultdict(lambda : 0 ) def contains (t_dict, count_dict ): if len (count_dict) < len (t_dict): return False for key in count_dict: if count_dict[key] < t_dict[key] or key not in t_dict: return False return True for right in range (length_s): if s[right] in t_dict: count_dict[s[right]] += 1 while left < length_s and contains(t_dict, count_dict): if right - left + 1 < len (result): result = s[left:right + 1 ] if s[left] in t_dict: count_dict[s[left]] -= 1 left += 1 return "" if result == s + s else result so = Solution1() print(so.minWindow1("ADOBECODEBANC" , "ABC" )) from typing import Listclass Solution : def combine (self, n: int , k: int ) -> List[List[int]]: if n <= 0 or k <= 0 or n < k: return [] result = [] self.__dfs(1 , k, n, [], result) return result def __dfs (self, index, k, n, pre, result ): if len (pre) == k: result.append(pre[:]) return for i in range (index, n + 1 ): pre.append(i) self.__dfs(i + 1 , k, n, pre, result) pre.pop() so = Solution() print(so.combine(4 , 2 ))
remove-duplicates-from-sorted-array-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from typing import Listclass Solution : def removeDuplicates (self, nums: List[int ] ) -> int: j, count = 1 , 1 for i in range (1 , len (nums)): if nums[i] == nums[i - 1 ]: count += 1 else : count = 1 if count <= 2 : nums[j] = nums[i] j += 1 return j so = Solution() print(so.removeDuplicates([0 , 0 , 1 , 1 , 1 , 1 , 2 , 3 , 3 ]))
interview_41 窗口何时扩大,何时缩小?
当窗口的和小于 target 的时候,窗口的和需要增加,所以要扩大窗口,窗口的右边界向右移动
当窗口的和大于 target 的时候,窗口的和需要减少,所以要缩小窗口,窗口的左边界向右移动
当窗口的和恰好等于 target 的时候,我们需要记录此时的结果。设此时的窗口为 [i, j),那么我们已经找到了一个 i 开头的序列,也是唯一一个 i 开头的序列,接下来需要找 i+1 开头的序列,所以窗口的左边界要向右移动。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from typing import Listclass Solution : def findContinuousSequence (self, target: int ) -> List[List[int]]: i = 1 j = 1 sum_current = 0 result = [] while i <= target // 2 : if sum_current < target: sum_current += j j += 1 elif sum_current > target: sum_current -= i i += 1 else : result.append(list (range (i, j))) sum_current -= i i += 1 return result so = Solution() print(so.findContinuousSequence(10 ))
interview_42 算法流程:
初始化: 双指针 i , j分别指向数组 nums 的左右两端 (俗称对撞双指针)。
循环搜索: 当双指针相遇时跳出;
计算和 s = nums[i] + nums[j];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 from typing import Listclass Solution : def twoSum (self, nums: List[int ], target: int ) -> List[int]: i, j = 0 , len (nums)-1 if j < 0 : return nums while i != j: if nums[i] + nums[j] > target: j -= 1 elif nums[i] + nums[j] < target: i += 1 else : return [nums[i], nums[j]] return [] so = Solution() print(so.twoSum([1 , 2 , 3 , 4 , 5 ], 7 ))
interview_64 如果使用暴力解法,可能会被面试官直接微笑回去等消息。即以下这种酸爽解法。
1 2 3 4 5 6 7 class Solution : def maxSlidingWindow (self, nums: List[int ], k: int ) -> List[int]: if len (nums) == 0 or k == 0 : return [] ans = [] for i in range (0 ,len (nums)-k+1 ): ans.append(max (nums[i:i+k])) return ans
为降低时间复杂度,此题难点是:
如何在每次窗口滑动后,将 “获取窗口内最大值” 的时间复杂度从 O(k) 降低至 O(1) 。
此题与interview_20(包含min函数的栈 )一起食用最佳。即:
维护一个队列。保持队列是单调递减,即加入时把前面比其小的数pop掉。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from typing import Listimport collectionsclass Solution : def maxSlidingWindow (self, nums: List[int ], k: int ) -> List[int]: if k == 0 : return [] de = collections.deque() result, len_nums = [], len (nums) for left, right in zip (range (1 - k, len_nums + 1 - k), range (len_nums)): if left > 0 and de[0 ] == nums[left-1 ]: de.popleft() while de and de[-1 ] < nums[right]: de.pop() de.append(nums[right]) if left >= 0 : result.append(de[0 ]) return result
Dynamic Programming wildcard-matching 解题思路:
true
false
false
false
false
true
false
false
false
false
true
true
false
false
false
true
false
false
false
true
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def isMatch (self, s: str , p: str ) -> bool: s_len = len (s) p_len = len (p) dp = [[False ] * (p_len + 1 ) for i in range (s_len + 1 )] dp[0 ][0 ] = True for i in range (1 , p_len + 1 ): if p[i-1 ] == "*" : dp[0 ][i] = dp[0 ][i-1 ] for i in range (1 , s_len + 1 ): for j in range (1 , p_len + 1 ): if s[i-1 ] == p[j-1 ] or p[j-1 ] == "?" : dp[i][j] = dp[i-1 ][j-1 ] elif p[j - 1 ] == "*" : dp[i][j] = dp[i-1 ][j] or dp[i][j-1 ] return dp[-1 ][-1 ] so = Solution() print(so.isMatch("adceb" , "*a*b" ))
maximum-subarray
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from typing import Listclass Solution : def maxSubArray_GA (self, nums: List[int ] ) -> int: len_nums = len (nums) current_sum = max_sum = nums[0 ] for i in range (1 , len_nums): current_sum = max (nums[i], current_sum + nums[i]) max_sum = max (max_sum, current_sum) return max_sum so = Solution() print(so.maxSubArray([-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 ]))
1 2 3 4 5 6 7 8 def maxSubArray_DP (self, nums: List[int ] ) -> int: len_nums = len (nums) max_sum = nums[0 ] for i in range (1 , len_nums): if nums[i-1 ] > 0 : nums[i] += nums[i-1 ] max_sum = max (max_sum, nums[i]) return max_sum
jump-game 解题思路:
从右向左迭代,对于每个节点我们检查是否存在一步跳跃可以到达 GOOD 的位置(currPosition + nums[currPosition] >= leftmostGoodIndex)。如果可以到达,当前位置也标记为 GOOD ,同时,这个位置将成为新的最左边的 GOOD 位置,一直重复到数组的开头,如果第一个坐标标记为 GOOD 意味着可以从第一个位置跳到最后的位置。
Index
0
1
2
3
4
Nums
2
0
1
1
4
Good/Bad
*Good
*Good
Good
*Good
Good
Good
False(1+0 < 2)
*Good(0+2 >= 2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from typing import Listclass Solution : def canJump (self, nums: List[int ] ) -> bool: last_true_index = nums[-1 ] for i in range (len (nums) - 1 , 0 , -1 ): if i + nums[i] >= last_true_index: last_true_index = nums[i] else : return False return True so = Solution() print(so.canJump([2 , 3 , 1 , 1 , 4 ]))
unique-paths 解题思路:
假设dp[row][col]代表到格子[i][j]的路径个数,其中第一行dp[0][j]与第一列dp[i][0]都为1。
那么每个格子的路径个数取决于它左边格子的路径个数+它上边格子的路径个数。
即dp[i][j]=dp[i][j-1]+dp[i-1][j]
为了节省空间,利用两个数组pre与cur来代表上一行与当前行。初始化都为1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def uniquePaths (self, m: int , n: int ) -> int: pre = [1 ] * n cur = [1 ] * n for row in range (1 , m): for col in range (1 , n): cur[col] = cur[col-1 ] + pre[col] pre = cur return pre[-1 ] so = Solution() print(so.uniquePaths(7 , 3 ))
unique-paths-ii 解题思路:
与上一题思路类似,让obstacleGrid存储到达各个单元的路径。
首先进行边界初始化,边界上的元素,只有自身为0(代表本身无障碍)且上一个单元值为1(已初始化,此时的1代表无障碍,有1条路可以通行)时,自身的值才被置为1(代表有路径可走)。
根据相邻单元的路径情况,进行自身路径的计算即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from typing import Listclass Solution : def uniquePathsWithObstacles (self, obstacleGrid: List[List[int ]] ) -> int: row = len (obstacleGrid) col = len (obstacleGrid[0 ]) if obstacleGrid[0 ][0 ] == 1 : return 0 obstacleGrid[0 ][0 ] = 1 for i in range (1 , col): obstacleGrid[0 ][i] = int (obstacleGrid[0 ][i-1 ] == 1 and obstacleGrid[0 ][i] == 0 ) for j in range (1 , row): obstacleGrid[j][0 ] = int (obstacleGrid[j-1 ][0 ] == 1 and obstacleGrid[j][0 ] == 0 ) print(obstacleGrid) for i in range (1 , row): for j in range (1 , col): if obstacleGrid[i][j] == 1 : obstacleGrid[i][j] = 0 else : obstacleGrid[i][j] = obstacleGrid[i-1 ][j] + obstacleGrid[i][j-1 ] return obstacleGrid[-1 ][-1 ] so = Solution() print(so.uniquePathsWithObstacles([ [0 , 0 , 0 ], [0 , 1 , 0 ], [0 , 0 , 0 ] ]))
minimum-path-sum 解题思路:
将Grid二维数组自身进行修改,使其存储当前元素到最右下角元素的路径值
从数组右下角元素开始遍历
最后一行的元素,路径等于自身加右侧的权值
除最后一行,其他行的最后一列,路径等于同列的下一行的权值加自身值
其他元素的路径,等于自身加上右侧权值与下侧路径的较小值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 from typing import Listclass Solution : def minPathSum (self, grid: List[List[int ]] ) -> int: row_len = len (grid) col_len = len (grid[0 ]) for row in range (row_len-1 , -1 , -1 ): for col in range (col_len-1 , -1 , -1 ): if row == row_len-1 and col != col_len-1 : grid[row][col] += grid[row][col+1 ] elif row != row_len-1 and col == col_len-1 : grid[row][col] += grid[row+1 ][col] elif row != row_len-1 and col != col_len-1 : grid[row][col] += min (grid[row+1 ][col], grid[row][col+1 ]) return grid[0 ][0 ] so = Solution() print(so.minPathSum([ [1 , 3 , 1 ], [1 , 5 , 1 ], [4 , 2 , 1 ] ])) 7
climbing-stairs dp用于存储到达每个台阶的方法总数。
则到达第n阶,有dp[i-1]+dp[i-2]种方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def climbStairs (self, n: int ) -> int: dp = [i for i in range (n)] dp[0 ] = 1 dp[1 ] = 2 for i in range (2 , n): dp[i] = dp[i-1 ] + dp[i-2 ] return dp[-1 ] so = Solution() print(so.climbStairs(3 ))
climbing-stairsII f(n)=f(n-1)+f(n-2)+……f(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def jumpFloorII (self, number ): if number <= 1 : return number n = 1 for i in range (2 , number+1 ): n = 2 * n return n
edit-distance 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def minDistance (self, word1: str , word2: str ) -> int: n1 = len (word1) n2 = len (word2) dp = [[0 ] * (n2+1 ) for _ in range (n1+1 )] for i in range (1 , n2 + 1 ): dp[0 ][i] = dp[0 ][i - 1 ] + 1 for j in range (1 , n1 + 1 ): dp[j][0 ] = dp[j - 1 ][0 ] + 1 for i in range (1 , n1 + 1 ): for j in range (1 , n2 + 1 ): if word1[i-1 ] == word2[j-1 ]: dp[i][j] = dp[i - 1 ][j - 1 ] else : dp[i][j] = min (dp[i - 1 ][j - 1 ], dp[i - 1 ][j], dp[i][j - 1 ]) + 1 return dp[-1 ][-1 ] so = Solution() print(so.minDistance(word1="horse" , word2="ros" ))
decode-ways 解题思路
dp[i+1]:代表s[0:i]的译码方式总数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def numDecodings (self, s: str ) -> int: if s[0 ] == "0" : return 0 dp = [1 , 0 ] dp[1 ] = 1 if s[0 ] != 0 else 0 n = len (s) for i in range (1 , n): dp.append(0 ) if s[i] != "0" : dp[i+1 ] += dp[i] if "10" <= s[i-1 :i+1 ] <= "26" : dp[i+1 ] += dp[i-2 ] return dp[-1 ] so = Solution() print(so.numDecodings("226" ))
interleaving-string dp[i][j]代表s1[:i]与s2[:j]能否构成s3[:i+j]
参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution : def isInterleave (self, s1: str , s2: str , s3: str ) -> bool: len_s1 = len (s1) len_s2 = len (s2) len_s3 = len (s3) if len_s1 + len_s2 != len_s3: return False dp = [[False for _ in range (len_s2+1 )] for _ in range (len_s1+1 )] dp[0 ][0 ] = True for j in range (1 , len_s2+1 ): dp[0 ][j] = True if s3[j-1 ] == s2[j-1 ] else False for i in range (1 , len_s1+1 ): dp[i][0 ] = True if s3[i-1 ] == s1[i-1 ] else False for i in range (1 , len_s1+1 ): for j in range (1 , len_s2+1 ): if dp[i-1 ][j] and s1[i-1 ] == s3[i+j-1 ]: dp[i][j] = True if dp[i][j-1 ] and s2[j-1 ] == s3[i+j-1 ]: dp[i][j] = True return dp[-1 ][-1 ] so = Solution() print(so.isInterleave(s1="aabcc" , s2="dbbca" , s3="aadbbcbcac" ))
split-array-with-equal-sum 参考链接
这道题确定i,j,k的取值范围是关键。
通过j去约定i和k的范围,可以减少复杂度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from typing import Listclass Solution : def splitArray (self, nums: List[int ] ) -> bool: len_nums = len (nums) if len_nums < 7 : return False sum_list = list () sum_list.append(nums[0 ]) for i in range (1 , len_nums): sum_list.append(sum_list[i - 1 ] + nums[i]) for j in range (3 , len_nums - 3 ): sum_set = set () for i in range (1 , j - 1 ): if sum_list[i - 1 ] == sum_list[j - 1 ] - sum_list[i]: sum_set.add(sum_list[i - 1 ]) for k in range (j + 2 , len_nums - 1 ): if sum_list[-1 ] - sum_list[k] == sum_list[k - 1 ] - sum_list[j] \ and (sum_list[k - 1 ] - sum_list[j]) in sum_set: return True return False so = Solution() print(so.splitArray([1 , 2 , 1 , 2 , 1 , 2 , 1 ]))
interview_33 解题思路
丑数的递推性质: 丑数只包含因子 2, 3, 5。因此有 “丑数 == 某较小丑数 × 某因子” (例如:10 = 5 ×2)
指针a,b,c分别代表*2、*3、*5的三个指针,它们指向的丑数一旦完成计算,则继续指向下一个丑数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution : def nthUglyNumber (self, n: int ) -> int: if n <= 0 : return 0 dp, a, b, c = [1 ] * n, 0 , 0 , 0 for i in range (1 , n): min_ugly = min (dp[a] * 2 , dp[b] * 3 , dp[c] * 5 ) dp[i] = min_ugly if min_ugly == dp[a] * 2 : a += 1 if min_ugly == dp[b] * 3 : b += 1 if min_ugly == dp[c] * 5 : c += 1 return dp[-1 ] so = Solution() print(so.nthUglyNumber(10 ))
interview_7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def fib (self, N: int ) -> int: if N <= 1 : return N f_dict = {0 : 0 , 1 : 1 } for i in range (2 , N): f_dict[i] = f_dict[i - 1 ] + f_dict[i - 2 ] return f_dict[N - 1 ] so = Solution() print(so.fib(4 ))
interview_8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def climbStairs (self, n: int ) -> int: if 0 <= n <= 2 : return n dp = [i for i in range (n)] dp[0 ] = 1 dp[1 ] = 2 for i in range (2 , n): dp[i] = dp[i - 1 ] + dp[i - 2 ] return dp[-1 ] so = Solution() print(so.climbStairs(3 ))
interview_9 用f(n)表示青蛙跳上n阶台阶的跳法数,设定f(0) = 1;
当n = 1 时,只有一种跳的方式,一阶跳,f(1) = 1
当n = 2 时,有两种跳的方式,一阶跳和两阶跳,f(2) = f(1) + f(0) = 2
当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有f(3-1)中跳法; 第一次跳出二阶后,后面还有f(3-2)中跳法;第一次跳出三阶后,后面还有f(3-3)种跳法,f(3) = f(2) + f(1) + f(0) = 4
当n = n 时,第一次跳出一阶后,后面还有f(n-1)中跳法; 第一次跳出二阶后,后面还有f(n-2)中跳法……第一次跳出n阶后,后面还有f(n-n)中跳法,即
f(n) = f(n-1) + f(n-2) + f(n-3) + ... + f(n-n) = f(0) + f(1) + f(2) + ... + f(n-1)
又因为f(n-1) = f(0) + f(2) + f(3) + ... + f(n-2)
两式相减得:f(n) = 2 * f(n-1) ( n >= 2)
| 0,n = 0
f(n) = | 1, n = 1
| 2 * f(n-1) , n >= 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def jumpFloorII (self, number ): if number <= 1 : return number n = 1 for i in range (2 , number + 1 ): n = 2 * n return n
interview_67 参考链接
方法一:暴力递归
时间复杂度:$O(2^N)$。
空间复杂度:$O(2^N)$。
设 F(n) 为长度为 n 的绳子可以得到的最大乘积,对于每一个 F(n),注意到我们每次将一段绳子剪成两段时,剩下的部分可以继续剪,也可以不剪 。这就得到了递归函数:
F(n) = max( i * ( n-i ) , i * F( n-1) ), i=1,2,…,n−2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def cuttingRope (self, n: int ) -> int: if n < 1 : return 0 if n == 1 or n == 2 : return 1 result = -1 for i in range (1 , n): result = max (result, max (i * (n-i), i * memorize(n - i))) return result
方法二:记忆化技术(自顶向下)
暴力法超时的原因是因为重复计算了F(N) ,为了避免重复计算可以使用 记忆化(memoization) 技术。
记忆化技术的代码中经常需要建立函数 memoize 辅助实现。我们使用数组 f 来保存长度为 i时的最大长度 f[i],最后返回 f[n]即可。
由于利用数组保存了中间结果,所以可以将空间复杂度降低至$O(N)$
时间复杂度:$O(2^N)$。
空间复杂度:$O(N)$。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution : def cuttingRope (self, n: int ) -> int: if n < 1 : return 0 def memorize (n ): if n == 2 : return 1 if fn[n] != 0 : return fn[n] result = -1 for i in range (1 , n): result = max (result, max (i * (n-i), i * memorize(n - i))) fn[n] = result return result fn = [0 for _ in range (n+1 )] return memorize(n) so = Solution() print(so.cuttingRope(10 ))
方法三:记忆化技术(自底向上)(推荐贪心法:简洁易懂)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def cuttingRope (self, n: int ) -> int: if n < 1 : return 0 dp = [0 for _ in range (n+1 )] dp[1 ] = 1 dp[2 ] = 1 for i in range (3 , n+1 ): for j in range (i): dp[i] = max (dp[i], max ((i - j) * j, dp[i - j] * j)) return dp[n] so = Solution() print(so.cuttingRope(10 ))
Greedy Algorithm jump-game-ii 本题使用贪心算法求解,寻找局部最优解 。
即在可跳范围内选择能跳的最远的位置
当前位置在“2”,可跳位置为“3”,“1”,其中可跳的最远的位置为“3”,则选择“3”
当前位置在“3”,可跳位置为“1”、“1”、“4”,其中可跳的最远的位置为“4”,则选择“4”
跳跃结束,step为2
步数
Step1
2(当前位置)
*3
*1
1
4
Step1
2
3(当前位置)
*1
*1
*4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 from typing import Listclass Solution : def jump (self, nums: List[int ] ) -> int: max_position = 0 end = 0 step = 0 if len (nums) < 2 : return step for i in range (len (nums)-1 ): max_position = max (max_position, nums[i] + i) if i == end: end = max_position step += 1 return step so = Solution() print(so.jump([2 , 3 , 1 , 1 , 4 ]))
maximum-subarray
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from typing import Listclass Solution : def maxSubArray_GA (self, nums: List[int ] ) -> int: len_nums = len (nums) current_sum = max_sum = nums[0 ] for i in range (1 , len_nums): current_sum = max (nums[i], current_sum + nums[i]) max_sum = max (max_sum, current_sum) return max_sum so = Solution() print(so.maxSubArray([-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 ]))
1 2 3 4 5 6 7 8 def maxSubArray_DP (self, nums: List[int ] ) -> int: len_nums = len (nums) max_sum = nums[0 ] for i in range (1 , len_nums): if nums[i-1 ] > 0 : nums[i] += nums[i-1 ] max_sum = max (max_sum, nums[i]) return max_sum
interview_30 此题同maximum_subarray
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from typing import Listclass Solution : def maxSubArray (self, nums: List[int ] ) -> int: if not nums: return 0 max_number = nums[0 ] for i in range (1 , len (nums)): nums[i] += max (nums[i-1 ], 0 ) max_number = max (max_number, nums[i]) return max_number so = Solution() print(so.maxSubArray([-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 ]))
merge-intervals 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 from typing import Listclass Solution : def merge (self, intervals: List[List[int ]] ) -> List[List[int]]: seq = sorted (intervals) i = 1 while i < len (seq): if seq[i-1 ][0 ] <= seq[i][0 ] <= seq[i-1 ][1 ]: if seq[i][1 ] > seq[i-1 ][1 ]: seq[i-1 ][1 ] = seq[i][1 ] seq.remove(seq[i]) else : i += 1 return seq so = Solution() print(so.merge([[1 , 3 ], [1 , 6 ], [1 , 80 ], [15 , 7 ]]))
insert-interval 参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from typing import Listclass Solution : def insert (self, intervals: 'List[Interval]' , newInterval: 'Interval' ) -> 'List[Interval]': start, end = newInterval current, n = 0 , len (intervals) output = [] while current < n and intervals[current][0 ] < start: output.append(intervals[current]) current += 1 if not output and output[-1 ][1 ] < start: output.append(newInterval) else : output[-1 ][1 ] = max (end, output[-1 ][1 ]) while current < n: if output[-1 ][1 ] < intervals[current][0 ]: output.append(intervals[current]) else : output[-1 ][1 ] = max (intervals[current][1 ], output[-1 ][1 ]) current += 1 return output so = Solution() print(so.insert([[1 , 2 ], [3 , 5 ], [6 , 7 ], [8 , 10 ], [12 , 16 ]], [4 , 8 ]))
queue-reconstruction-by-height 这道题的关键思想是官网所说的:“因为个子矮的人相对于个子高的人是 “看不见” 的,所以可以先安排个子高的人。”
即,先按照身高对每个人进行排序,然后再根据个子矮的人所对应的索引,插入到个子高的人中,因为个子矮的人相对于个子高的人是 “看不见” 的,所以插入过程中并不会影响前面已经排好序的个子高的人。
过程如下:具体解题思路 见官网。
排序:
按高度降序排列。
在同一高度的人中,按 k 值的升序排列。
逐个地把它们放在输出队列中,索引等于它们的 k 值。
返回输出队列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from typing import Listclass Solution : def reconstructQueue (self, people: List[List[int ]] ) -> List[List[int]]: people.sort(key=lambda x: (-x[0 ], x[1 ]), reverse=False ) out_put_people = [] for person in people: out_put_people.insert(person[1 ], person) return out_put_people so = Solution() print(so.reconstructQueue([[7 , 0 ], [4 , 4 ], [7 , 1 ], [5 , 2 ], [6 , 1 ], [5 , 0 ]]))
remove-duplicate-letters 参考链接
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def removeDuplicateLetters (self, s: str ) -> str: if s == "" : return s stack = [] value_in_stack = set () last_occurance = {k:i for i, k in enumerate (s)} for i, c in enumerate (s): if c not in value_in_stack: while stack and stack[-1 ] > c and last_occurance[stack[-1 ]] > i: value_in_stack.discard(stack.pop()) stack.append(c) value_in_stack.add(c) return "" .join(stack) so = Solution() print(so.removeDuplicateLetters("cbacdcbc" ))
String 在合并两个数组或者字符串时,如果从前往后复制每个数字(或者字符)需要重复移动数字(或字符)多次,则可以考虑从后往前复制,就能减少移动的次数。
3_length_of_longest_substring 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 import timeitclass Solution : def lengthoflongestsubstring (self, s: str ) -> int: tem_length = 0 max_length = 0 s_set = set () for i in range (len (s)): if s[i] in s_set: s_set.remove(s[i]) tem_length = 0 else : s_set.add(s[i]) tem_length += 1 if tem_length > max_length: max_length = tem_length return max_length if __name__ == "__main__" : so = Solution() test_list = "pwdflkkkpwdsadf" start = timeit.default_timer() print(so.lengthoflongestsubstring(test_list)) end = timeit.default_timer() print(str ((end - start) * 1000 ), "s" )
valid-number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import reclass Solution : def isNumber (self, s: str ) -> bool: s = s.strip() if not s: return False if s[0 ] in ["+" , "-" ]: s = s[1 :] if "e" in s: s_list = s.split("e" ) if len (s_list) > 2 : return False s_list[0 ] = s_list[0 ].replace("." , "" , 1 ) if len (s_list[1 ]) > 0 and s_list[1 ][0 ] in ["+" , "-" ]: s_list[1 ] = s_list[1 ].replace(s_list[1 ][0 ], "" , 1 ) if s_list[0 ].isnumeric() and s_list[1 ].isnumeric(): return True else : s = s.replace("." , "" , 1 ) if s.isnumeric(): return True return False so = Solution() print(so.isNumber("53.5e93" ))
text-justification 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 from typing import Listclass Solution : def fullJustify (self, words: List[str ], maxWidth: int ) -> List[str]: if not words: return [] result = [] current_chars_number = 0 current_words_number = 0 word_list = [] for index, value in enumerate (words): current_word_length = len (value) if current_chars_number + current_word_length + current_words_number > maxWidth: if current_words_number == 1 : result.append(word_list[0 ] + " " * (maxWidth - current_chars_number)) else : blank_space_number = maxWidth - current_chars_number if blank_space_number % (current_words_number - 1 ) == 0 : result.append((" " * (blank_space_number // (current_words_number - 1 ))).join(word_list)) else : more_blankspace = blank_space_number % (current_words_number - 1 ) stand_blankspace = blank_space_number // (current_words_number - 1 ) res = word_list[0 ] for i in range (more_blankspace): res += " " * (stand_blankspace+1 ) + word_list[i+1 ] for i in range (more_blankspace+1 , len (word_list)): res += " " * stand_blankspace + word_list[i] result.append(res) current_chars_number = current_word_length current_words_number = 1 word_list = [value] else : current_chars_number += current_word_length current_words_number += 1 word_list.append(value) return result so = Solution() print(so.fullJustify(["This" , "is" , "an" , "example" , "of" , "text" , "justification." ], 16 ))
simplify-path 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution : def simplifyPath (self, path: str ) -> str: if not path: return "" result_list = [] path = path.split("/" ) for value in path: if value == ".." : if result_list: result_list.pop() elif value and value != "." : result_list.append(value) return "/" + "/" .join(result_list) so = Solution() print(so.simplifyPath("/a/./b/../../c/" ))
Interview_2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution : def replaceSpace (self, s: str ) -> str: return s.replace(" " , "%20" ) so = Solution() print(so.replaceSpace("We are happy." ))
这里用list而不是str直接处理的原因是。str是不可变数据类型,也就是说每在一个str后面加了一个字符,都是新的str。这样导致空间开销太大。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def replaceSpace (self, s: str ) -> str: s_list = list () for s_value in s: if s_value == " " : s_list.append("%20" ) else : s_list.append(s_value) return "" .join(s_list) so = Solution() print(so.replaceSpace("We are happy." ))
interview_43 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def reverseLeftWords (self, s: str , n: int ) -> str: len_s = len (s) if n >= len_s or n <= 0 : return s return s[n:] + s[:n] so = Solution() print(so.reverseLeftWords("abcdefg" , 2 ))
interview_44 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def reverseWords (self, s: str ) -> str: if not s: return s s_rotate = s.split() if len (s_rotate) <= 1 : return s return " " .join(s_rotate[::-1 ]) so = Solution() print(so.reverseWords("abc bvc nbm" ))
interview_45 先对数组执行排序
判别重复: 排序数组中的相同元素位置相邻,因此可通过遍历数组,判断 nums[i] = nums[i + 1]是否成立来判重。
获取最大 / 最小的牌: 排序后,数组末位元素 nums[4] 为最大牌;元素 nums[joker]为最小牌,其中 joker为大小王的数量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 from typing import Listclass Solution : def isStraight (self, nums: List[int ] ) -> bool: if not nums: return False joker = 0 nums.sort() for i in range (len (nums) - 1 ): if nums[i] == 0 : joker += 1 elif nums[i] == nums[i + 1 ]: return False return nums[4 ] - nums[joker] < 5 so = Solution() print(so.isStraight([0 , 0 , 1 , 2 , 5 ]))
Sort introduction
排序算法
平均时间复杂度
最差时间复杂度
额外空间复杂度
稳定性
备注
冒泡排序
$o(n^2)$
$o(n^2)$
$o(1)$
稳定
n小时效果好
选择排序
$o(n^2)$
$o(n^2)$
$o(1)$
不稳定
n小时效果好
交换排序
$o(n^2)$
$o(n^2)$
$o(1)$
不稳定
n小时效果好
插入排序
$o(n^2)$
$o(n^2)$
$o(1)$
稳定
n小时效果好
快速排序
$o(nlogn)$
$o(n^2)$
$o(nlogn)-o(n)$
不稳定
n大时效果好
归并排序
$o(nlogn)$
$o(nlogn)$
$o(n)$
稳定
n大时效果好
堆排序
$o(nlogn)$
$o(nlogn)$
$o(1)$
不稳定
n大时效果好
希尔排序
$o(nlogn)$
$o(n^s)$ 1<s<2
$o(1)$
不稳定
s是所选分组
基数排序
$o(log_RB)($线性复杂度)
$o(log_RB)$
$o(n)$
稳定
B是真数(0-9),R是基数(个十百)
计数排序
$o(n)$
$o(nlogn)$
稳定
0
划分排序
$o(n)$
0
0
稳定
0
桶排序
$o(n)$
0
0
稳定
0
https://leetcode-cn.com/problems/sort-an-array/solution/python-shi-xian-de-shi-da-jing-dian-pai-xu-suan-fa/
桶排序 冒泡排序 快速排序 堆排序 堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
归并排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 def mergesort (seq ): """归并排序""" if len (seq) <= 1 : return seq mid = len (seq) / 2 left = mergesort(seq[:mid]) right = mergesort(seq[mid:]) return merge(left, right) def merge (left, right ): """合并两个已排序好的列表,产生一个新的已排序好的列表""" result = [] i = 0 j = 0 while i < len (left) and j < len (right): if left[i] <= right[j]: result.append(left[i]) i += 1 else : result.append(right[j]) j += 1 result += left[i:] result += right[j:] return result seq = [5 ,3 ,0 ,6 ,1 ,4 ] print '排序前:' ,seqresult = mergesort(seq)
largest-number 自定义排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from typing import Listclass LargerNumKey (str def __lt__ (x, y ): return x + y < y + x class Solution : def largestNumber (self, nums ): return_value = "" .join(sorted (map (str , nums), key=LargerNumKey, reverse=True )).lstrip("0" ) return "0" if return_value[0 ] == "0" else return_value so = Solution() print(so.largestNumber([3 , 30 , 34 , 5 , 9 ]))
interview_32 同上一题:largest-number,这题不加任何技巧。类似于冒泡排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 from typing import Listclass Solution (object def minNumber (self, nums ): """ :type nums: List[int] :rtype: str """ if not nums: return None for i in range (len (nums)): nums[i] = str (nums[i]) for i in range (len (nums)): for j in range (i + 1 , len (nums)): if (nums[i] + nums[j]) > (nums[j] + nums[i]): nums[i], nums[j] = nums[j], nums[i] return '' .join(nums) so = Solution() print(so.minNumber([3 , 30 , 34 , 5 , 9 ]))
Top-K Sort kth-largest-element-in-an-array 堆排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 from typing import Listimport heapqclass Solution : def findKthLargest (self, nums: List[int ], k: int ) -> int: return heapq.nlargest(k, nums)[-1 ] so = Solution() print(so.findKthLargest([3 , 2 , 1 , 5 , 6 , 4 ], 2 ))
interview_29 解题思路
方法一:堆排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 from typing import Listimport heapqclass Solution : def findKthLargest (self, arr: List[int ], k: int ) -> int: len_tinput = len (tinput) if k > len_tinput: return [] return heapq.nsmallest(k, arr) so = Solution() print(so.findKthLargest([3 , 2 , 1 , 5 , 6 , 4 ], 2 ))
方法2:利用快速排序思想
这个 partition 操作是原地进行的,需要 O(n)的时间,接下来,快速排序会递归地排序左右两侧的数组。而快速选择(quick select)算法的不同之处在于,接下来只需要递归地选择一侧的数组。快速选择算法想当于一个“不完全”的快速排序,因为我们只需要知道最小的 k 个数是哪些,并不需要知道它们的顺序。
我们的目的是寻找最小的 k 个数。假设经过一次 partition 操作,枢纽元素位于下标 m,也就是说,左侧的数组有 m 个元素,是原数组中最小的 m 个数。那么:
若 k = m,我们就找到了最小的 k 个数,就是左侧的数组;
若 k < m ,则最小的 k 个数一定都在左侧数组中,我们只需要对左侧数组递归地 parition 即可;
若 k > m,则左侧数组中的 m 个数都属于最小的 k 个数,我们还需要在右侧数组中寻找最小的 k-m 个数,对右侧数组递归地 partition 即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 from typing import Listclass Solution : def getLeastNumbers (self, arr: List[int ], k: int ) -> List[int]: if k <= 0 or k > len (arr): return [] start = 0 end = len (arr) - 1 pivot = self.quicksort(arr, start, end) while pivot != k - 1 : if pivot > k - 1 : end = pivot - 1 pivot = self.quicksort(arr, start, end) if pivot < k - 1 : start = pivot + 1 pivot = self.quicksort(arr, start, end) return arr[:k] def quicksort (self, arr, left, right ): """ 简单版快速排序 返回一个坐标,坐标左侧都小于返回值,右侧都大于返回值 """ i = left j = right temp = arr[left] while i < j: while i < j and arr[j] >= temp: j -= 1 arr[i] = arr[j] while i < j and arr[i] < temp: i += 1 arr[j] = arr[i] arr[i] = temp return i so = Solution() print(so.getLeastNumbers([4 , 5 , 1 , 6 , 2 ], 4 ))
sort-an-array 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 from typing import Listclass Solution : def sortArray (self, nums: List[int ] ) -> List[int]: if not nums: return [] n = len (nums) def quick (left, right ): if left >= right: return nums pivot = left i = left j = n - 1 while i < j: while i < j and nums[j] > nums[pivot]: j -= 1 while i < j and nums[i] <= nums[pivot]: i += 1 nums[i], nums[j] = nums[j], nums[i] nums[pivot], nums[j] = nums[j], nums[pivot] quick(left, j-1 ) quick(j+1 , right) return nums return quick(0 , n - 1 ) so = Solution() print(so.sortArray([5 , 1 , 1 , 2 , 0 , 0 ]))
maximum-gap 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from typing import Listclass Solution : def maximumGap (self, nums: List[int ] ) -> int: len_nums = len (nums) if len_nums < 2 : return 0 nums.sort(reverse=False ) max_gap = abs (nums[1 ] - nums[0 ]) for i in range (2 , len_nums): max_gap = max (max_gap, abs (nums[i] - nums[i - 1 ])) return max_gap so = Solution() print(so.maximumGap([3 , 6 , 9 , 1 ]))
contains-duplicate 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 from typing import Listclass Solution : def containsDuplicate (self, nums: List[int ] ) -> bool: if not nums: return False nums.sort(reverse=False ) for i in range (1 , len (nums)): if nums[i] == nums[i-1 ]: return True return False so = Solution() print(so.containsDuplicate([1 , 2 , 3 , 1 , 2 , 3 ]))
contains-duplicate-ii 用散列表来维护这个k大小的滑动窗口。
遍历数组,对于每个元素做以下操作:
返回 false。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 from typing import Listclass Solution : def containsNearbyDuplicate (self, nums: List[int ], k: int ) -> bool: nums_sort = list () nums_sort.append(nums[0 ]) for i in range (1 , len (nums)): if nums[i] in nums_sort: return True elif len (nums_sort) >= k: nums_sort.pop(0 ) nums_sort.append(nums[i]) return False so = Solution() print(so.containsNearbyDuplicate([1 , 2 , 3 , 4 , 2 , 3 ], 2 ))
contains-duplicate-iii 方法一:线性搜索,超时
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from typing import Listclass Solution : def containsNearbyAlmostDuplicate (self, nums: List[int ], k: int , t: int ) -> bool: if len (nums) <= 1 : return False nums_sort = list () nums_sort.append(nums[0 ]) for i in range (1 , len (nums)): if len (nums_sort) > k: nums_sort.pop(0 ) tmp_nums_sored = sorted (nums_sort, reverse=False ) for v in tmp_nums_sored: if abs (nums[i] - v) <= t: return True nums_sort.append(nums[i]) return False so = Solution() print(so.containsNearbyAlmostDuplicate(nums=[1 , 5 , 9 , 1 , 5 , 9 ], k=2 , t=3 ))
方法二:桶排序
由于本题对索引有要求,考虑使用桶排序。
每个数字nums[i] 都被分配到一个桶中
每个桶序号代表存放t的倍数的数 nums[i] // (t + 1)
不相邻的桶一定不满足相差小于等于t,且同一个桶内的数字最多相差t
因此如果命中同一个桶内,那么直接返回True
如果命中相邻桶,我们再判断一下是否满足相差 <= t
题目有索引相差k的要求,因此要维护一个大小为k的窗口,定期清除桶中过期的数字。bucket.pop(nums[i - k] // (t + 1)) 即清除当前i前的第k个元素所对应的桶序号。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 from typing import Listclass Solution : def containsNearbyAlmostDuplicate (self, nums: List[int ], k: int , t: int ) -> bool: bucket = dict () if t < 0 : return False for i in range (0 , len (nums)): bucket_nth = nums[i] // (t + 1 ) if bucket_nth in bucket: return True if bucket_nth - 1 in bucket and abs (bucket[bucket_nth - 1 ] - nums[i]) <= t: return True if bucket_nth + 1 in bucket and abs (bucket[bucket_nth + 1 ] - nums[i]) <= t: return True bucket[bucket_nth] = nums[i] if i >= k: bucket.pop(nums[i - k] // (t + 1 )) return False so = Solution() print(so.containsNearbyAlmostDuplicate(nums=[1 , 5 , 9 , 1 , 5 , 9 ], k=2 , t=3 ))
interview_63 参考链接
复杂度分析:
时间复杂度:
空间复杂度 O(N): 其中 N 为数据流中的元素数量,小顶堆 B 和大顶堆 A最多同时保存 N 个元素。
算法利用大顶堆A和小顶堆B,A存放较小的元素,B存放较大的元素。使得B的最小的元素也比A中最大的元素大,保证数据流保持有序。
B保持比A多一个的状态 ,当数据流长度时为奇数时,则向A中插入元素;偶数时,则向B中插入元素。
Python 中 heapq 模块是小顶堆。实现 大顶堆 方法: 小顶堆的插入和弹出操作均将元素 取反 即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 e: interview_63.py from heapq import *class MedianFinder : def __init__ (self ): """ initialize your data structure here. """ self.A = [] self.B = [] def addNum (self, num: int ) -> None : if len (self.A) != len (self.B): heappush(self.B, num) heappush(self.A, -heappop(self.B)) else : heappush(self.A, -num) heappush(self.B, -heappop(self.A)) def findMedian (self ) -> float: if len (self.A) != len (self.B): return self.B[0 ] else : return (-self.A[0 ] + self.B[0 ]) / 2.0
Math interview_12 1 2 3 4 2^3 2^3 = 2^1 * 2^1 * 2 2^1 = 2^0 * 2 2^0 = 1
1 2 3 4 5 2^4 2^4 = 2^2 * 2^2 2^2 = 2^1 * 2^1 2^1 = 2^0 * 2 2^0 = 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def myPow (self, x: float , n: int ) -> float: if n == 0 : return 1 if n == -1 : return 1 / x half = self.myPow(x, n // 2 ) if n % 2 == 0 : return half * half else : return half * half * x so = Solution() print(so.myPow(2.00000 , -10 ))
Other remove-duplicates-from-sorted-array 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def removeDuplicates (self, nums ): if len (nums) == 0 : return 0 i = 0 for j in range (1 , len (nums)): if nums[i] != nums[j]: i += 1 nums[i] = nums[j] return i + 1 so = Solution() print(so.removeDuplicates([0 , 0 , 1 , 1 , 1 , 2 , 2 , 3 , 3 , 4 ]))
remove-element 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def removeElement (self, nums, val: int ): if not nums: return 0 i = 0 for j in range (0 , len (nums)): if nums[j] != val: nums[i] = nums[j] i += 1 return i so = Solution() print(so.removeElement([0 , 1 , 2 , 2 , 3 , 0 , 4 , 2 ], 2 ))
implement-strstr 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def strStr (self, haystack: str , needle: str ) -> int: if len (haystack) < len (needle): return -1 j = 0 for i in range (0 , len (haystack) - len (needle) + 1 ): index = i for j in range (0 , len (needle)): if haystack[i] != needle[j]: break i += 1 if j == len (needle) - 1 : return index return -1 so = Solution() print(so.strStr("hello" , "ll" ))
substring-with-concatenation-of-all-words 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 class Solution (object def findSubstring (self, s, words ): """ :type s: str :type words: List[str] :rtype: List[int] """ if len (s) == 0 or not words: return [] words_number = len (words) words_len = len (words[0 ]) s_len = len (s) word_dic = {} for word in words: if word in word_dic.keys(): word_dic[word] += 1 else : word_dic[word] = 1 output_list = [] for i in range (words_len): start_index = i s_cut_list = [] cut_number = 0 while s_len - start_index >= words_len: s_cut_list.append(s[start_index : start_index + words_len]) cut_number += 1 start_index += words_len start_cut_i = 0 while cut_number - start_cut_i > words_number: count = 0 w_dic = {} for s_word in s_cut_list[start_cut_i : start_cut_i + words_number]: if s_word in word_dic.keys(): if s_word in w_dic.keys(): w_dic[s_word] += 1 if w_dic[s_word] > word_dic[s_word]: break count += 1 else : w_dic[s_word] = 1 count += 1 else : break if count == words_number: output_list.append(i + start_cut_i * words_len) start_cut_i += 1 return output_list so = Solution() print(so.findSubstring("barfoothefoobarman" , ["foo" , "bar" ]))
next-permutation 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution : def nextPermutation (self, nums ) -> None : """ Do not return anything, modify nums in-place instead. """ if not nums: return [] left = -1 for i in range (len (nums) - 1 , 0 , -1 ): if nums[i - 1 ] < nums[i]: left = i - 1 break if left == -1 : return nums[::-1 ] for right in range (len (nums) - 1 , left, -1 ): if nums[right] > nums[left]: nums[right], nums[left] = nums[left], nums[right] break nums_left = nums[left + 1 : len (nums)] nums_left = nums_left[::-1 ] nums[left + 1 : len (nums)] = nums_left return nums so = Solution() print(so.nextPermutation([1 , 2 , 3 , 7 , 4 ]))
longest-valid-parentheses 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution : def longestValidParentheses (self, s: str ) -> int: if not s or len (s) == 1 : return 0 maxlen = 0 left, right = 0 , 0 for i in range (len (s)): if s[i] == "(" : left += 1 else : right += 1 if left == right: maxlen = right * 2 if maxlen < right * 2 else maxlen elif right > left: left = right = 0 left, right = 0 , 0 for i in range (len (s) - 1 , -1 , -1 ): if s[i] == "(" : left += 1 else : right += 1 if left == right: maxlen = left * 2 if maxlen < left * 2 else maxlen elif left > right: left = right = 0 return maxlen so = Solution() print(so.longestValidParentheses("())((())" ))
search-insert-position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def searchInsert (self, nums, target: int ) -> int: for i in range (0 , len (nums) - 1 ): if nums[i] == target: return i elif nums[i] < target <= nums[i + 1 ]: return i + 1 elif nums[i] > target: return -1 return len (nums) so = Solution() print(so.searchInsert([1 , 3 , 5 , 6 ], 7 ))
combination-sum-ii 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 from typing import Listclass Solution : def combinationSum (self, candidates: List[int ], target: int ) -> List[List[int]]: if not candidates or not target: return [] candidates.sort() output_list = [] path = [] begin = 0 size = len (candidates) self._dfs(candidates, begin, size, path, output_list, target) return output_list def _dfs (self, candidates, begin, size, path, output_list, target ): if target == 0 : output_list.append(path[:]) for index in range (begin, size): residue = target - candidates[index] if residue < 0 : break if index > begin and candidates[index - 1 ] == candidates[index]: continue path.append(candidates[index]) self._dfs(candidates, index+1 , size, path, output_list, residue) path.pop() if __name__ == '__main__' : candidates = [2 , 5 , 2 , 1 , 2 ] target = 5 solution = Solution() result = solution.combinationSum(candidates, target) print(result)
multiply-strings 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def multiply (self, num1: str , num2: str ) -> str: if num1 == '0' or num2 == '0' : return 0 return_sum = 0 count = 0 for val1 in num2[::-1 ]: add = 0 multiply_sum = 0 count1 = 0 for val2 in num1[::-1 ]: multi_sum = (int (val1) * int (val2) + add) % 10 multiply_sum += multi_sum * (10 ** count1) add = (int (val1) * int (val2) + add) // 10 count1 += 1 return_sum += multiply_sum * (10 ** count) count += 1 return str (return_sum) so = Solution() print(so.multiply("123" , "456" ))
group-anagrams 解题方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import collectionsclass Solution : def groupAnagrams (self, strs ): ans = collections.defaultdict(list ) for s in strs: ans[tuple (sorted (s))].append(s) return ans.values() so = Solution() print(so.groupAnagrams(["eat" , "tea" , "tan" , "ate" , "nat" , "bat" ]))
plus-one 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from typing import Listclass Solution : def plusOne (self, digits: List[int ] ) -> List[int]: if not digits: return [] len_digits = len (digits) add = (digits[len_digits-1 ] + 1 ) // 10 digits[len_digits-1 ] = (digits[len_digits-1 ] + 1 ) % 10 for i in range (len_digits - 2 , -1 , -1 ): add = (digits[i] + add) // 10 digits[i] = (digits[i] + add) % 10 if add == 1 : digits.insert(0 , add) return digits so = Solution() print(so.plusOne([9 , 9 , 9 , 9 ]))
length-of-last-word 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution : def lengthOfLastWord (self, s: str ) -> int: if not s: return 0 return len (s.split()[-1 ]) so = Solution() print(so.lengthOfLastWord("Hello World" ))
permutation-sequence 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 import mathclass Solution : def getPermutation (self, n: int , k: int ) -> str: nums = [str (i) for i in range (1 , n + 1 )] output_str = "" n -= 1 while n > -1 : number_combination = math.factorial(n) output_number_index = math.ceil(k / number_combination) - 1 output_str += nums[output_number_index] nums.pop(output_number_index) k %= number_combination n -= 1 return output_str so = Solution() print(so.getPermutation(4 , 9 ))
6_convert 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution : def convert (self, s: str , numRows: int ) -> str: if not s: return "" elif len (s) == 1 : return s outstr = ["" ] * numRows i = 0 while i < len (s): for j in range (0 , numRows): if i < len (s): outstr[j] += s[i] i += 1 for j in range (numRows - 2 , 0 , -1 ): if i < len (s): outstr[j] += s[i] i += 1 outstr = "" .join(outstr) return outstr s = "ABCDE" so = Solution() print(so.convert(s, 3 ))
7_reverse-integer 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution : def reverse (self, x: int ) -> int: if not x: return x len_x = len (str (x)) reverse_x = "" for i in range (0 , len_x): middle_x = (x % pow (10 , i + 1 )) // pow (10 , i) reverse_x = reverse_x + str (middle_x) return reverse_x s = 123456789 so = Solution() print(so.reverse(s))
palindrome_number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution : def isPalindrome (self, x: int ) -> bool: if x < 0 or (x % 10 == 0 and x != 0 ): return False return_num = 0 while x > return_num: return_num = return_num * 10 + x % 10 x = x // 10 return x == return_num or x == return_num // 10 so = Solution() print(so.isPalindrome(1221 ))
container-with-most-water 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution : def maxArea (self, height ) -> int: if not height: return 0 i, j = 0 , len (height) - 1 max_size = 0 while i < j: if height[i] < height[j]: tmp_size = (j - i) * height[i] i += 1 else : tmp_size = (j - i) * height[j] j -= 1 max_size = tmp_size if tmp_size > max_size else max_size return max_size so = Solution() assert so.maxArea([1 , 8 , 6 , 2 , 5 , 4 , 8 , 3 , 7 ])
integer-to-roman 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution : def intToRoman (self, num: int ) -> str: output = "" roman_dict = { 1000 : "M" , 900 : "CM" , 500 : "D" , 400 : "CD" , 100 : "C" , 90 : "XC" , 50 : "L" , 40 : "XL" , 10 : "X" , 9 : "IX" , 5 : "V" , 4 : "IV" , 1 : "I" , } while num > 0 : for key, value in roman_dict.items(): if num >= key: output += value num -= key break return output so = Solution() print(so.intToRoman(999 ))
roman-to-integer 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution : def romanToInt (self, s ): output = 0 roman_dict = {"I" : 1 , "V" : 5 , "X" : 10 , "L" : 50 , "C" : 100 , "D" : 500 , "M" : 1000 } for i in range (len (s)): if i < len (s) - 1 and roman_dict[s[i]] < roman_dict[s[i + 1 ]]: output -= roman_dict[s[i]] else : output += roman_dict[s[i]] return output so = Solution() print(so.romanToInt("MCMXCIV" ))
longest-common-prefix 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def longestCommonPrefix (self, li ) -> str: if not li: return "" min_str = min (li) max_str = max (li) for index, value in enumerate (min_str): if value != max_str[index]: return max_str[:index] return min_str so = Solution() print(so.longestCommonPrefix(["flower" , "flow" , "flight" ]))
3sum 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution : def threeSum (self, nums ): if not nums or len (nums) < 3 : return [] n = len (nums) output = [] nums.sort() for i in range (0 , n): if nums[i] > 0 : return output if i > 0 and nums[i] == nums[i - 1 ]: continue left = i + 1 right = n - 1 while left < right: if nums[i] + nums[left] + nums[right] == 0 : output.append((nums[i], nums[left], nums[right])) while left < right and nums[left] == nums[left + 1 ]: left += 1 while left < right and nums[right] == nums[right - 1 ]: right -= 1 left += 1 right -= 1 elif nums[i] + nums[left] + nums[right] > 0 : right -= 1 else : left += 1 return output so = Solution() print(so.threeSum([-1 , 0 , 1 , 2 , -1 , -4 ]))
3sum-closest 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution : def threeSumClosest (self, nums, target ) -> int: if not nums or len (nums) < 3 : return 0 nums.sort() n = len (nums) result = nums[0 ] + nums[1 ] + nums[2 ] for i in range (0 , n - 2 ): left = i + 1 right = n - 1 while left < right: min_value = nums[i] + nums[left] + nums[left + 1 ] if target < min_value: if abs (min_value - target) < abs (result - target): result = min_value break max_value = nums[i] + nums[right] + nums[right - 1 ] if target > max_value: if abs (max_value - target) < abs (result - target): result = max_value break sum_value = nums[i] + nums[left] + nums[right] if abs (sum_value - target) < abs (result - target): result = sum_value if sum_value == target: return sum_value if sum_value > target: right -= 1 while (not left == right) and nums[right] == nums[right + 1 ]: right -= 1 else : left += 1 while (not left == right) and nums[left] == nums[left - 1 ]: left += 1 while i < n - 2 and nums[i] == nums[i + 1 ]: i += 1 return result so = Solution() print(so.threeSumClosest([-1 , 2 , 1 , -4 ], 1 ))
letter-combinations-of-a-phone-number 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution : def letterCombinations (self, digits: str ): digit_number_dict = { "2" : ["a" , "b" , "c" ], "3" : ["d" , "e" , "f" ], "4" : ["g" , "h" , "i" ], "5" : ["j" , "k" , "l" ], "6" : ["m" , "n" , "o" ], "7" : ["p" , "q" , "r" , "s" ], "8" : ["t" , "u" , "v" ], "9" : ["w" , "x" , "y" , "z" ], } output = [] def backtrack (combination, next_digits ): if not next_digits: output.append(combination) else : for letter in digit_number_dict[next_digits[0 ]]: backtrack(combination + letter, next_digits[1 :]) if digits: backtrack("" , digits) return output so = Solution() print(so.letterCombinations("27" ))
4Sum 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Solution : def fourSum (self, nums, target ): nums = sorted (nums) if len (nums) < 4 : return [] elif sum (nums[:4 ]) > target: return [] n = len (nums) result_li = [] for i in range (n - 2 ): for left in range (i + 1 , n - 1 ): middle = left + 1 right = n - 1 while middle != right: sum_value = nums[i] + nums[left] + nums[middle] + nums[right] if ( sum_value == target and [nums[i], nums[left], nums[middle], nums[right]] not in result_li ): result_li.append( [nums[i], nums[left], nums[middle], nums[right]] ) if sum_value <= target: middle += 1 while middle != right and nums[middle] == nums[middle - 1 ]: middle += 1 else : right -= 1 while middle != right and nums[right] == nums[right + 1 ]: right -= 1 return result_li so = Solution() print(so.fourSum([1 , 0 , -1 , 0 , -2 , 2 ], 0 ))
remove-nth-node-from-end-of-list 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class ListNode : def __init__ (self, x ): self.val = x self.next = None class Solution : def removeNthFromEnd (self, head: ListNode, n: int ) -> ListNode: head_pre = ListNode(-1 ) head_pre.next , start, end = head, head_pre, head_pre while end and n > 0 : end = end.next if not end: return head while end.next : start, end = start.next , end.next start.next = start.next .next return head
3_length_of_longest_substring 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 import timeitclass Solution : def lengthoflongestsubstring (self, s: str ) -> int: tem_length = 0 max_length = 0 s_set = set () for i in range (len (s)): if s[i] in s_set: s_set.remove(s[i]) tem_length = 0 else : s_set.add(s[i]) tem_length += 1 if tem_length > max_length: max_length = tem_length return max_length if __name__ == "__main__" : so = Solution() test_list = "pwdflkkkpwdsadf" start = timeit.default_timer() print(so.lengthoflongestsubstring(test_list)) end = timeit.default_timer() print(str ((end - start) * 1000 ), "s" )
88_merge-sorted-array 解题思路:
初阶版 — 合并后排序
时间复杂度 : O((n + m)log(n + m))、空间复杂度O(1)
1 2 3 4 5 6 7 8 9 10 from typing import Listclass Solution : def merge (self, nums1: List[int ], m: int , nums2: List[int ], n: int ) -> List: """ Do not return anything, modify nums1 in-place instead. """ nums1[:] = sorted (nums1[:m], nums2) return nums1
进阶版:双指针/从前往后
最直接的算法实现是将指针p1 置为 nums1的开头, p2为 nums2的开头,在每一步将最小值放入输出数组中。
由于 nums1 是用于输出的数组,需要将nums1中的前m个元素放在其他地方,也就需要 O(m)O(m) 的空间复杂度。
时间复杂度 : O(n + m)、空间复杂度O(m)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution (object def merge (self, nums1, m, nums2, n ): """ :type nums1: List[int] :type m: int :type nums2: List[int] :type n: int :rtype: void Do not return anything, modify nums1 in-place instead. """ nums1_copy = nums1[:m] nums1[:] = [] p1 = 0 p2 = 0 while p1 < m and p2 < n: if nums1_copy[p1] < nums2[p2]: nums1.append(nums1_copy[p1]) p1 += 1 else : nums1.append(nums2[p2]) p2 += 1 if p1 < m: nums1[p1 + p2:] = nums1_copy[p1:] if p2 < n: nums1[p1 + p2:] = nums2[p2:]
高阶版:三指针/从后往前
p1、p2分别指向nums1、nums2当前准备移动的元素。p指向当前待放置的位置。
哪个指向的数字大,则将其放置于p所指的位置上。
时间复杂度 : O(n + m)、空间复杂度O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from typing import Listclass Solution : def merge (self, nums1: List[int ], m: int , nums2: List[int ], n: int ) -> List: """ Do not return anything, modify nums1 in-place instead. """ if not nums1: return nums2 if not nums2: return nums1 p1 = m - 1 p2 = n - 1 p = m + n - 1 while p1 >= 0 and p2 >= 0 : if nums1[p1] < nums2[p2]: nums1[p] = nums2[p2] p2 -= 1 else : nums1[p] = nums1[p1] p1 -= 1 p -= 1 nums1[:p2 + 1 ] = nums2[:p2 + 1 ] return nums1 so = Solution() print(so.merge(nums1=[1 , 2 , 3 , 0 , 0 , 0 ], m=3 , nums2=[2 , 5 , 6 ], n=3 ))
reOrderArray 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def reOrderArray (self, array ): len_array = len (array) if len_array <= 1 : return array left = 0 right = len_array - 1 while left <= right: if array[left] & 1 == 0 : array.append(array.pop(left)) right -= 1 else : left += 1 return array so = Solution() print(so.reOrderArray([1 , 2 , 3 , 4 , 5 ]))
interview_31 写不动写不动,太难了。直接暴力吧。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def countDigitOne (self, n: int ) -> int: s = "" while n: s += str (n) n -= 1 return s.count("1" ) so = Solution() print(so.countDigitOne(12 ))
interview_13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution : def reOrderArray (self, array ): len_array = len (array) if len_array <= 1 : return array left = 0 right = len_array - 1 while left <= right: if array[left] & 1 == 0 : array.append(array.pop(left)) right -= 1 else : left += 1 return array so = Solution() print(so.reOrderArray([1 , 2 , 3 , 4 , 5 ]))
interview_40 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution : def FindNumsAppearOnce (self, array ): if not array: return [] len_array = len (array) if len_array <= 3 : return [] result = [] array.sort() i, j = 0 , 1 for j in range (1 , len_array): if array[i] != array[j]: if j - i == 1 : result.append(array[i]) i = j if array[-1 ] != array[-2 ]: result.append(array[-1 ]) return "," .join(str (_) for _ in result) so = Solution() print(so.FindNumsAppearOnce([2 , 4 , 3 , 6 , 3 , 2 , 5 , 5 ]))
interview_46 暴力法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution : def lastRemaining (self, n: int , m: int ) -> int: if n == 0 : return -1 i, array = 0 , list (range (n)) while len (array) > 1 : i = (i + m - 1 ) % len (array) array.pop(i) return array[0 ] so = Solution() print(so.lastRemaining(5 , 3 ))
interview_47 短路思想
以逻辑运算符 & 为例,对于 A & B 这个表达式,如果 A 表达式返回 False ,那么 A & B 已经确定为 False ,此时不会去执行表达式 B。同理,对于逻辑运算符 ||, 对于 A || B 这个表达式,如果 A 表达式返回 True ,那么 A || B 已经确定为 True ,此时不会去执行表达式 B。
利用这一特性,我们可以将判断是否为递归的出口看作 A & B 表达式中的 A 部分,递归的主体函数看作 B 部分。如果不是递归出口,则返回True,并继续执行表达式 B 的部分,否则递归结束。
递归思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution : def __init__ (self ): self.res = 0 def sumNums (self, n: int ) -> int: n > 1 and self.sumNums(n - 1 ) self.res += n return self.res so = Solution() print(so.sumNums(3 ))
interview_54 Insert函数用来接收字符,构成字符流。
FirstAppearingOnce函数用来判断是否为第一个只出现一次的字符。用了字典来记录字符以及出现的次数。
由于python的dict不是按照时间顺序来存储的,所以需要借助一个数组来记录。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def __init__ (self ): self.char_appearing_dict = {} self.char_insert = [] def FirstAppearingOnce (self ): if not self.char_appearing_dict: return "#" for c in self.char_insert: if self.char_appearing_dict[c] == 1 : return c return "#" def Insert (self, char ): self.char_insert.append(char) if char in self.char_appearing_dict: self.char_appearing_dict[char] += 1 else : self.char_appearing_dict[char] = 1